题目内容
设命题p:函数g(x)=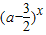 是R上的减函数,命题q:函数
是R上的减函数,命题q:函数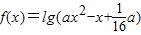 的定义域为R,若“p且q”为假命题,“p或q”为真命题,求实数a的取值范围.
的定义域为R,若“p且q”为假命题,“p或q”为真命题,求实数a的取值范围.
【答案】分析:先化简命题p、q,再根据“p且q”为假命题,“p或q”为真命题,等价于 或
或
进而可求出a的取值范围.
解答:解:由命题p:函数g(x)= 是R上的减函数,∴0<
是R上的减函数,∴0< <1,解得
<1,解得 .
.
由命题q:当a≤0时,函数 的定义域不为R,应舍去;
的定义域不为R,应舍去;
当a>0时,要使函数 的定义域为R,即对任意实数都满足
的定义域为R,即对任意实数都满足 ,
,
则必有△<0,即1 ,又a>0,解得a>2.
,又a>0,解得a>2.
由已知“p且q”为假命题,“p或q”为真命题,等价于 或
或
由 得到
得到 ;
;
由 得到a≥
得到a≥ .
.
综上可知:a的取值范围是: 或
或 .
.
点评:本题考查了函数的性质和复合命题的真假,充分理解性质及判断方法是解决问题的关键.
 或
或
进而可求出a的取值范围.
解答:解:由命题p:函数g(x)=
 是R上的减函数,∴0<
是R上的减函数,∴0< <1,解得
<1,解得 .
.由命题q:当a≤0时,函数
 的定义域不为R,应舍去;
的定义域不为R,应舍去;当a>0时,要使函数
 的定义域为R,即对任意实数都满足
的定义域为R,即对任意实数都满足 ,
,则必有△<0,即1
 ,又a>0,解得a>2.
,又a>0,解得a>2.由已知“p且q”为假命题,“p或q”为真命题,等价于
 或
或
由
 得到
得到 ;
;由
 得到a≥
得到a≥ .
.综上可知:a的取值范围是:
 或
或 .
.点评:本题考查了函数的性质和复合命题的真假,充分理解性质及判断方法是解决问题的关键.

练习册系列答案
相关题目
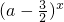 是R上的减函数,命题q:函数
是R上的减函数,命题q:函数 的定义域为R,若“p且q”为假命题,“p或q”为真命题,求实数a的取值范围.
的定义域为R,若“p且q”为假命题,“p或q”为真命题,求实数a的取值范围.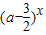 是R上的减函数,命题q:函数
是R上的减函数,命题q:函数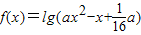 的定义域为R,若“p且q”为假命题,“p或q”为真命题,求实数a的取值范围.
的定义域为R,若“p且q”为假命题,“p或q”为真命题,求实数a的取值范围.