题目内容
已知二次函数y=kx2-kx-2的图象与x轴没有交点,求k的取值范围.分析:y=kx2-kx-2的图象与x轴无交点,当图象在x轴上方时,
,当图象在x轴下方时,
,由此能够求出k的取值范围.
|
|
解答:解:∵y=kx2-kx-2的图象与x轴无交点,
∴当图象在x轴上方时,
,∴
,解为空集.
当图象在x轴下方时,
,∴
,∴-8<k<0.
∴k的取值范围是{k|-8<k<0}.
∴当图象在x轴上方时,
|
|
当图象在x轴下方时,
|
|
∴k的取值范围是{k|-8<k<0}.
点评:本题考查二次函数的图象和性质,解题时要抓住二次函数与x轴无交点的特点进行求解.

练习册系列答案
相关题目
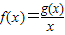 .
. ,求m的值;
,求m的值;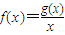 .
.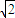 ,求m的值;
,求m的值; .
.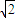 ,求m的值;
,求m的值;