题目内容
14.已知奇函数f(x)的定义域为R,若f(x+1)为偶函数,且f(1)=1,则f(2016)+f(2015)=( )| A. | -2 | B. | -1 | C. | 0 | D. | 1 |
分析 根据f(x)和f(x+1)的奇偶性便可得到f(x)=f(x-1+1)=f(x-4),从而得出f(x)是周期为4的周期函数,而可以求出f(2)=0,从而可以得出f(2016)+f(2015)=f(2)-f(1)=-1.
解答 解:∵f(x)为R上的奇函数,f(x+1)为偶函数,
∴f(x)=f(x-1+1)=f(-x+2)=-f(x-2)=f(x-4);
∴f(x)是周期为4的周期函数;
∴f(2016)+f(2015)=f(2+503×4)+f(-1+504×4)=f(2)-f(1)=f(2)-1;
f(-1+1)=f(1+1)=0;
即f(2)=0;
∴f(2014)+f(2015)=0-1=-1.
故选:B.
点评 考查奇函数、偶函数的定义,以及周期函数的定义,清楚偶函数的定义:f(-x)=f(x),是自变量换上-x后函数值不变.

练习册系列答案
相关题目
9.已知命题p:函数f(x)=sinxcosx的单调递增区间[$kπ-\frac{π}{4}$,$kπ+\frac{π}{4}$](k∈Z);命题q:函数g(x)=sin(x+$\frac{π}{2}$) 的图象关于原点对称,则下列命题中为真命题的是( )
| A. | p∧q | B. | p∨q | C. | -p | D. | (-p)∨q |
19.函数y=f(x)处处可导且对任意x∈R,f′(x)>0恒成立,当x1<x2时,f′(x1)>f′(x2),则下列叙述正确的是( )
| A. | 函数y=f(x)单调递增且图象向下凹陷 | B. | 函数y=f(x)单调递减且图象向上凸起 | ||
| C. | 函数y=f(x)单调递减且图象向下凹陷 | D. | 函数y=f(x)单调递增且图象向上凸起 |
3.平行四边形ABCD中,AC与BD交于点O,M为OC的中点,若$\overrightarrow{AB}$=(2,4),$\overrightarrow{AC}$=(1,3),则$\overrightarrow{AD}•\overrightarrow{BM}$等于( )
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | 3 | D. | -3 |
 如图边长为2的正方形内部有一块不规则的区域E,若向该图中随机撒100颗豆子,经清点落在E内的有30颗,试估计E的面积为:1.2.
如图边长为2的正方形内部有一块不规则的区域E,若向该图中随机撒100颗豆子,经清点落在E内的有30颗,试估计E的面积为:1.2.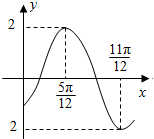 函数f(x)=2sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则f(0)的值是-$\sqrt{3}$.
函数f(x)=2sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则f(0)的值是-$\sqrt{3}$.