题目内容
求下列函数的最小正周期
(1)y＝tan
－
；
(2)y＝2|sin(4x－
)|；
(3)y＝(asin＋cosx)2(a∈R)；
(4)y＝2cosxsin(x＋)－
sin2x＋sinxcosx
答案：
解析：
解析：
|
解答 (1)因为y＝tan ＝ 所以此函数的最小正周期为π． (2)注意到y＝sin(4x－ (3)因为y＝[ ＝(a2＋1)sin2(x＋ ＝(a2＋1)· 所以此函数的最小正周期为 (4)因为y＝2cosx( ＝sinxcosx＋ ＝sin2x＋ 所以该函数的最小正周期是T＝ 评析 求三角函数最小正周期的基本方法有两种：一是将所给函数化为y＝Asin(ωx＋ |
－
－
＝－
＝－cotx
)的最小正周期T＝
＝
，结合y＝2|sin(4x－
)|的图象，知其最小正周期为
×
．
sin(x＋
)]2
(
＝π
sinx＋
cosx)－
sin2x＋sinxcosx
cos2x－
sin2x＋sinxcosx
cos2x＝2sin(2x＋
)，
＝π．
求解；二是利用图象的基本特征求解．
练习册系列答案
名校课堂系列答案
相关题目
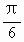)sin(kx＋
)，k≠0；
．
πx；
x)cos[
(x－1)]；
．
x－1)；
．
);
x-
).