Question

函数f（x）=x³-3tx+m（x∈R，m和t为常数）是奇函数．
（1）求实数m的值和函数f（x）的图象与横轴的交点坐标；
（2）设g（x）=|f（x）|（x∈[-1，1]），求g（x）的最大值F（t）；
（3）求F（t）的最小值．

Answer 1

分析：（1）先根据奇函数的性质求出m的值，然后结合函数的单调性，令f（x）=0即可求出x的值，从而求出与x轴的交点坐标．
（2）g（x）=|x³-3xt|（x∈[0，1]）是偶函数，所以只要求出g（x）=|x³-3xt|（x∈[0，1]）的最大值即可．
（3）F（t）在（-∞，

1

4

）上为减函数，

在[ 1 4 ，+∞)为增函数

，所以t=

1

4

时，F（t）取得最小值．

解答：解：（1）由于f（x）为奇函数，易得m=0…（1分）
设f（x）=x³-3tx=x（x²-3t）=0
①当3t＜0时，上述方程只有一个实数根x=0，所以f（x）与x轴的交点坐标为（0，0）
②当3t=0时，上述方程有三个相等实数根x=0，所以f（x）与x轴的交点坐标为（0，0）
③当3t＞0时，上述方程的解为x₁=0，x_2，3=±

3t

，所以f（x）与横轴的交点坐标分别为：（0，0），（

3t

，0)，(-

3t

，0）…（4分）（少一种情况扣1分）
（2）显然g（x）=|x³-3xt|（x∈[0，1]）是偶函数，
所以只要求出g（x）=|x³-3xt|（x∈[0，1]）的最大值即可．又f'（x）=3（x²-t）
①t≤0时，则在[0，1]上f（x）为增函数，∴f（x）≥f（0）=0∴f（x）=g（x），故F（t）=f（1）=1-3t…（6分）
②t＞0时，则在[0，1]上f'（x）=3（x+

t

)(x-

t

）
（i）

t

≥1即t≥1时，则在[0，1]上f（x）为减函数∴f（x）≤f（0）=0，

&∴g(x)=-f(x)，

故F（t）=-f（1）=3t-1…（8分）
（ii）0＜t＜1时，则在[0，1]上f'（x）=3（x+

t

)(x-

t

）

x	0	（0， t ）	t	（ t ，1）	1
f'（x）		-	0	+
f（x）	0	↓	极小值-2t t	↑	1-3t

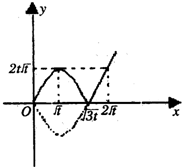
所以可以画出g（x）的草图如下，并且由图可知：

（1⁰）当

t

＜1≤2

t

即

1

4

≤t＜1时，g(x)的最大值F(t)=-f(

t

)=2t

t

（2⁰）当1＞2

t

即0＜t＜

1

4

时，g（x）的最大值F（t）=f（1）=1-3t…（10分）
综上所述：F（t）=

1-3t(t＜ 1 4 ) 2t t ( 1 4 ≤t＜1) 3t-1(t≥1)

…（12分）
（3）显然F（t）在（-∞，

1

4

）上为减函数，

在[ 1 4 ，+∞)为增函数

∴F（t）的最小值=F（

1

4

)=

1

4

．

点评：本题主要考查了三次函数的奇偶性，单调性等有关知识，考查了利用导数研究函数的最值，属于基础题．