题目内容
1.某天下午要排物理、化学、生物和两节自习共5节课,如果第一节不排生物,最后一节不排物理,那么不同的排法共有( )| A. | 36种 | B. | 39种 | C. | 60种 | D. | 78种 |
分析 利用排除法进行求解即可.
解答 解:若第一节排生物,有${A}_{4}^{2}$=12种方法,
第五节排物理,有${A}_{4}^{2}$=12种方法,
若第一节排生物,第五节排物理,有${A}_{3}^{1}$=3种方法,
第一节不排生物,第五节不排物理共有${A}_{5}^{3}$-2${A}_{4}^{2}$+${A}_{3}^{1}$=60-24+3=39种方法.
故选:B
点评 本题主要考查排列组合的计算问题,根据特殊元素的满足的条件,利用分类讨论和排除法是解决本题的关键.

练习册系列答案
相关题目
13.等比数列{an}中,a2=$\frac{1}{4}$,a6=4,记{an}的前n项积为Tn,则T7=( )
| A. | 1 | B. | 1或一1 | C. | 2 | D. | 2或一2 |
12.实数x,y满足$\left\{\begin{array}{l}{2x-y≥0}\\{y≥x}\\{y≥-x+b}\end{array}\right.$,则z=2x+y的最小值为3,则实数b的值为( )
| A. | $\frac{4}{9}$ | B. | -$\frac{4}{9}$ | C. | $\frac{9}{4}$ | D. | -$\frac{9}{4}$ |
10.命题p:关于x的方程x|x|-2x+m=0(m∈R)有三个实数根;命题q:0≤m<1;则命题p成立是命题q成立的( )
| A. | 充分而不必要的条件 | B. | 必要而不充分的条件 | ||
| C. | 充要条件 | D. | 既不充分又不必要的条件 |
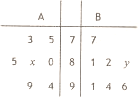 某学校从A、B两个班级中各选出7名学生参加市级比赛,他们去得的成绩(满分100分)的茎叶如图所示,其中A班学生成绩的众数是85,B班学生成绩的中位数是83.则x+y的值为8.
某学校从A、B两个班级中各选出7名学生参加市级比赛,他们去得的成绩(满分100分)的茎叶如图所示,其中A班学生成绩的众数是85,B班学生成绩的中位数是83.则x+y的值为8.