Question

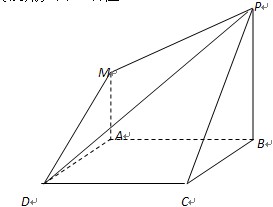
如图，四边形ABCD是正方形，PB^平面ABCD，MA∥PB，PB＝AB＝2MA．

（Ⅰ）证明：AC∥平面PMD；

（Ⅱ）求直线BD与平面PCD所成的角的大小；

（Ⅲ）求平面PMD与平面ABCD所成的二面角（锐角）的正切值．

Answer 1

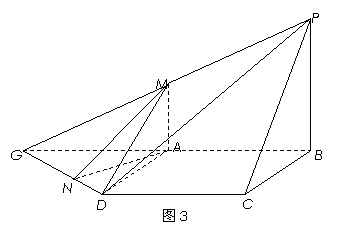
（Ⅰ）证明：如图，取PD的中点E，连EO，EM．

∵EO∥PB，EO＝PB，MA∥PB，MA＝PB，∴EO∥MA，且EO＝MA．

∴四边形MAOE是平行四边形．∴ME∥AC．

又∵AC平面PMD，MEÌ平面PMD，  ∴AC∥平面PMD．                 …………3分

（Ⅱ）如图，PB^平面ABCD，CDÌ平面ABCD，∴CD^PB．

又∵CD^BC，∴CD^平面PBC．  ∵CDÌ平面PCD，∴平面PBC^平面PCD．

过B作BF^PC于F，则BF^平面PDC，连DF，则DF为BD在平面PCD上的射影．

∴ÐBDF是直线BD与平面PDC所成的角．

不妨设AB＝2，则在Rt△PBC中，PB＝BC＝2，BF^PC，∴BF＝PC＝．

∵BD＝2．∴在Rt△BFD中，BF＝BD，∴ÐBDF＝．

∴直线BD与平面PCD所成的角是．                                ………………5分

（Ⅲ）解：如图，分别延长PM，BA，设PM∩BA＝G，连DG，

则平面PMD∩平面ABCD＝DG．

不妨设AB＝2，∵MA∥PB，PB＝2MA，∴GA＝AB＝2．

过A作AN^DG于N，连MN．  ∵PB^平面ABCD，

∴MA^平面ABCD，∴MN^DG．∴ÐMNA是平面PMD与平面ABCD

所成的二面角的平面角（锐角）．在Rt△MAN中，

tanÐMNA＝＝．

∴平面PMD与平面ABCD所成的二面角的正切值是