题目内容
利用单调函数的定义证明：函数f（x）=x+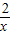
在区间（0，
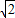）上是减函数．
【答案】分析：设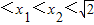 
，化简f（x1）-f（x2） 为
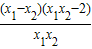，判断它的符号大于零，再根据减函数的定义得出结论．
解答：证明：设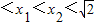
，（1分）
则 f（x1）-f（x2）=（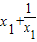
）-（
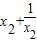）=（x1-x2 ）+2（
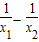） （4分）
=
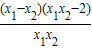（6分）
由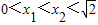
可得 0＜x1x2＜2，x1-x2＜0．
∴
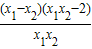＞0，即 f（x1）＞f（x2），
由单调函数的定义可知，函数函数f（x）=x+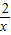
在区间（0，
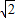）上是减函数．（12分）
点评：本题主要考查函数的单调性的判断和证明，属于基础题．
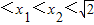，化简f（x1）-f（x2） 为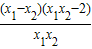，判断它的符号大于零，再根据减函数的定义得出结论．解答：证明：设
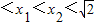，（1分）则 f（x1）-f（x2）=（
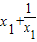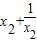）-（）=（x1-x2 ）+2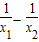（） （4分）=
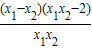（6分）由
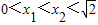可得 0＜x1x2＜2，x1-x2＜0． ∴
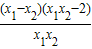＞0，即 f（x1）＞f（x2），由单调函数的定义可知，函数函数f（x）=x+
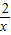在区间（0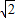，）上是减函数．（12分）点评：本题主要考查函数的单调性的判断和证明，属于基础题．
练习册系列答案
暑假作业海燕出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目