题目内容
已知直线l的参数方程为 ,(t为参数,α为倾斜角,且
,(t为参数,α为倾斜角,且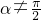 )与曲线
)与曲线 =1交于A,B两点.
=1交于A,B两点.
(Ⅰ)写出直线l的一般方程及直线l通过的定点P的坐标;
(Ⅱ)求|PA||PB|的最大值.
证明:(Ⅰ)∵直线的参数方程为 ,(t为参数,α为倾斜角,且
,(t为参数,α为倾斜角,且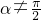 ),
),
所以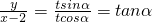 ,∴直线l的一般方程xtanα-y-2tanα=0,
,∴直线l的一般方程xtanα-y-2tanα=0,
直线l通过的定点P的坐标为(2,0).
(Ⅱ)∵l的参数方程为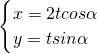 ,而椭圆方程为
,而椭圆方程为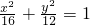 ,右焦点坐标为P(2,0)
,右焦点坐标为P(2,0)
∴3(2+tcosα)2+4(tsinα)2-48=0,即(3+sin2α)t2+12cosαt-36=0
∵直线l过椭圆的右焦点,∴直线与椭圆有两个交点.
∴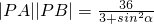 ,又α为倾斜角,且
,又α为倾斜角,且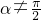
∴0≤sin2α<1,∴|PA||PB|的最大值为12.
故答案为12.
分析:(Ⅰ)首先可以分析到题目中的直线方程是参数方程的形式,需要化简为一般方程,第1问即可求得.
(Ⅱ)直线与曲线交与交于A,B两点,可以把直线与曲线联立方程,用根与系数关系即可得到求解.
点评:此题主要考查直线参数方程化一般方程,及直线与曲线相交的问题,在此类问题中一般可用联立方程式后用韦达定理求解即可,属于综合性试题有一定的难度.
 ,(t为参数,α为倾斜角,且
,(t为参数,α为倾斜角,且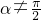 ),
),所以
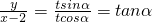 ,∴直线l的一般方程xtanα-y-2tanα=0,
,∴直线l的一般方程xtanα-y-2tanα=0,直线l通过的定点P的坐标为(2,0).
(Ⅱ)∵l的参数方程为
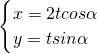 ,而椭圆方程为
,而椭圆方程为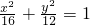 ,右焦点坐标为P(2,0)
,右焦点坐标为P(2,0)∴3(2+tcosα)2+4(tsinα)2-48=0,即(3+sin2α)t2+12cosαt-36=0
∵直线l过椭圆的右焦点,∴直线与椭圆有两个交点.
∴
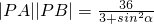 ,又α为倾斜角,且
,又α为倾斜角,且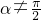
∴0≤sin2α<1,∴|PA||PB|的最大值为12.
故答案为12.
分析:(Ⅰ)首先可以分析到题目中的直线方程是参数方程的形式,需要化简为一般方程,第1问即可求得.
(Ⅱ)直线与曲线交与交于A,B两点,可以把直线与曲线联立方程,用根与系数关系即可得到求解.
点评:此题主要考查直线参数方程化一般方程,及直线与曲线相交的问题,在此类问题中一般可用联立方程式后用韦达定理求解即可,属于综合性试题有一定的难度.

练习册系列答案
相关题目