题目内容

已知数列{a_n}满足a₁=15，且a_n+1-a_n=2n，则 $数学公式$ 的最小值为________．

$\text{[math]}$
分析：利用叠加法求数列的通项，再根据基本不等式，即可求得 $\text{[math]}$ 的最小值．
解答：∵a₁=15，a_n+1-a_n=2n，
∴a_n=a₁+（a₂-a₁）+（a₃-a₂）+…+（a_n-a_n-1）=15+2+4+…+2（n-1）=15+2× 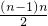$\text{[math]}$ =n²-n+15
∴ $\text{[math]}$ = $\text{[math]}$ -1
∵函数在[1，3]上单调递减，在[4，+∞）上单调递增
∵n=3时， $\text{[math]}$ =3+5-1=7；n=4时， $\text{[math]}$ =4+ $\text{[math]}$ -1= $\text{[math]}$
∴ $\text{[math]}$ 的最小值为 $\text{[math]}$
故答案为： $\text{[math]}$
点评：本题考查数列递推式，考查叠加法的运用，考查函数的单调性，属于中档题．

练习册系列答案

名师手把手系列答案

星际培优测试系列答案

新编助学读本系列答案

数学课堂与感悟系列答案

单元双测专题期中期末大试卷系列答案

金点考单元同步检测系列答案

素质目标检测系列答案

每课100分系列答案

智慧学习导学练系列答案

学科王同步课时练习系列答案

相关题目

已知数列{a_n}满足：a₁=1且an+1=

， n∈N*．
（1）若数列{b_n}满足：bn=

(n∈N*)，试证明数列b_n-1是等比数列；
（2）求数列{a_nb_n}的前n项和S_n；
（3）数列{a_n-b_n}是否存在最大项，如果存在求出，若不存在说明理由．

已知数列{a_n}满足

an=2n+1则{a_n}的通项公式

已知数列{a_n}满足：a₁=

（n≥2，n∈N^*）．
（1）求数列{a_n}的通项公式；
（2）证明：对于一切正整数n，不等式a₁•a₂•…a_n＜2•n！

已知数列{a_n}满足a_n+1=|a_n-1|（n∈N^*）
（1）若a1=

，求a_n；
（2）若a₁=a∈（k，k+1），（k∈N^*），求{a_n}的前3k项的和S_3k（用k，a表示）

（2012•北京模拟）已知数列{a_n}满足a_n+1=a_n+2，且a₁=1，那么它的通项公式a_n等于