题目内容
 将全体正整数排成一个三角形数阵:按照排列的规律,从左向右数,193是某行的第
将全体正整数排成一个三角形数阵:按照排列的规律,从左向右数,193是某行的第3
3
个数.分析:找出前n-1行正整数的个数,确定第n行第1个数是全体正整数中第
+1个,从而可得结论.
| n2-n |
| 2 |
解答:解:前n-1行共有正整数1+2+…+(n-1)个,即
个,
因此第n行第1个数是全体正整数中第
+1个,
当n=20时,
+1=191,
∴193是第20行的第3个数
故答案为:3
| n2-n |
| 2 |
因此第n行第1个数是全体正整数中第
| n2-n |
| 2 |
当n=20时,
| n2-n |
| 2 |
∴193是第20行的第3个数
故答案为:3
点评:本题考查归纳推理.归纳推理的一般步骤是:(1)通过观察个别情况发现某些相同性质;(2)从已知的相同性质中推出一个明确表达的一般性命题(猜想).

练习册系列答案
相关题目
将全体正整数排成一个三角形数阵:
1
2 3
4 5 6
7 8 9 10
…
按照以上排列的规律,第n 行(n≥3)从左向右的第3 个数为( )
1
2 3
4 5 6
7 8 9 10
…
按照以上排列的规律,第n 行(n≥3)从左向右的第3 个数为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
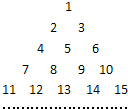 将全体正整数排成一个三角形数阵:按照以上排列的规律,第n行(n≥3)从左向右的第3个数为
将全体正整数排成一个三角形数阵:按照以上排列的规律,第n行(n≥3)从左向右的第3个数为 将全体正整数排成一个三角形数阵:
将全体正整数排成一个三角形数阵: