题目内容
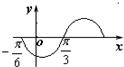已知函数f（x）=cos（ωx+?）（ω＞0，0＜?＜2π）的导函数f′（x）的图象如图所示，则?=（ ）A、
| ||
B、
| ||
C、
| ||
D、
|
分析：求出函数f（x）=cos（ωx+?）（ω＞0，0＜?＜2π）的导函数f′（x），结合导函数的图象，求出T，ω，图象经过（
，0）代入方程，求出?即可．
| π |
| 3 |
解答：解：函数f（x）=cos（ωx+?）（ω＞0，0＜?＜2π）的导函数f′（x）=-ωsin（ωx+?），
由题意可知T=π，所以ω=2
函数经过（
，0），
即：0=-2sin（
+?）；
所以?=
．
故选B
由题意可知T=π，所以ω=2
函数经过（
| π |
| 3 |
即：0=-2sin（
| 2π |
| 3 |
所以?=
| π |
| 3 |
故选B
点评：本题是基础题，考查由y=Asin（ωx+φ）的部分图象确定其解析式，注意复合函数的导数的求法，点在曲线上，点的坐标适合方程，考查计算能力．
练习册系列答案
相关题目
已知函数f（x）=
，则关于x的方程f2（x）+bf（x）+c=0有5个不同实数解的充要条件是（ ）
|
| A、b＜-2且c＞0 |
| B、b＞-2且c＜0 |
| C、b＜-2且c=0 |
| D、b≥-2且c=0 |
已知函数f（x）的图象如图所示，则函数的值域为（ ）