题目内容
已知函数f(x)=x|x-a|(a∈R).(1)判断f(x)的奇偶性;
(2)解关于x的不等式:f(x)≥2a2.
解析:(1)当a=0时,
f(-x)=-x|-x|=-x|x|=-f(x),
∴f(x)是奇函数.
当a≠0时,f(a)=0且f(-a)=-2a|a|.
故f(-a)≠f(a)且f(-a)≠-f(a).
∴f(x)是非奇非偶函数.
(2)由题设知x|x-a|≥2a2,
∴原不等式等价于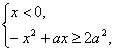 ①
①
或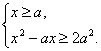 ②
②
由①得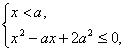 x∈
x∈![]() .
.
由②得![]()
当a=0时,x≥0;
当a>0时,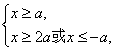
∴x≥2a.
当a<0时,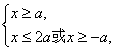 即x≥-a.
即x≥-a.
综上a≥0时,f(x)≥2a2的解集为{x|x≥2a};
a<0时,f(x)≥2a2的解集为{x|x≥-a}.

练习册系列答案
相关题目