题目内容
是椭圆的左焦点，
是椭圆上一点，
轴，
，
求椭圆的离心率。
解析:
设椭圆的方程为：
，∵
轴，∴
，
，∴
，
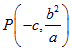，又
，∴
，∴
，∴。
练习册系列答案
云南师大附小一线名师提优作业系列答案
冲刺100分单元优化练考卷系列答案
相关题目
解析:
云南师大附小一线名师提优作业系列答案冲刺100分单元优化练考卷系列答案题目内容
是椭圆的左焦点，是椭圆上一点，轴，，求椭圆的离心率。
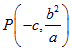设椭圆的方程为：，∵轴，∴，，∴，，又，∴，∴，∴。
云南师大附小一线名师提优作业系列答案冲刺100分单元优化练考卷系列答案
的离心率为
，以该椭圆上的点和椭圆的
为顶点的三角形的周长为
.一等轴双曲线的顶点是该椭
为该双曲线上异于顶点的任一点，直线
和
与椭圆的交点
和
（Ⅰ）求椭圆和双曲线的标准方程； 
、
，证明
；
，使得
恒成立？
上一点P到其左准线的距离为10,F是该椭圆的左焦点，若点M满足
（其中O为坐标原点），则
=_________
（a＞b＞0）的左、右两个焦点，椭圆C上的点
到两点的距离之和等于4．
求|PQ|的最大值．
的长轴长是焦距的两倍，其左、右焦点依次为
、
，抛物线
的准线与
轴交于
的一个交点为
.
时，求椭圆
过焦点
两点，若弦长
等于
的周长，求直线
和椭圆弧
）合成的曲线叫“抛椭圆”,是否存在以原点
为直角顶点，另两个顶点
落在“抛椭圆”上的等腰直角三角形
，若存在，求出两直角边所在直线的斜率；若不存在，说明理由.