Question

如图,四棱锥P-ABCD中，底面ABCD是平行四边形，∠ACB＝90°，平面PAD⊥平面ABCD，

PA=BC=1，PD=AB=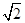,E、F分别为线段PD和BC的中点．

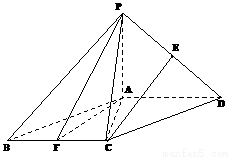
（Ⅰ） 求证：CE∥平面PAF；

（Ⅱ）在线段BC上是否存在一点G，使得平面PAG和平面PGC所成二面角的大小为60°？若存在，试确定G的位置；若不存在，请说明理由．

 

Answer 1

【答案】

（Ⅰ）先证明EC∥HF即可              （Ⅱ）存在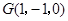

【解析】

试题分析：（1）取PA中点为H，连结CE、HE、FH，

因为H、E分别为PA、PD的中点，所以HE∥AD,,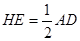

因为ABCD是平行四边形，且F为线段BC的中点 , 所以FC∥AD,

所以HE∥FC, 四边形FCEH是平行四边形 ,所以EC∥HF

又因为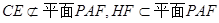   

所以CE∥平面PAF.        

（2）因为四边形ABCD为平行四边形且∠ACB＝90°，

所以CA⊥AD ,又由平面PAD⊥平面ABCD可得 CA⊥平面PAD , 

所以CA⊥PA , 由PA=AD=1，PD=可知，PA⊥AD,                   

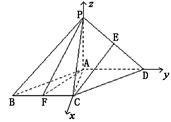
所以可建立如图所示的平面直角坐标系A-xyz, 因为PA=BC=1，AB=所以AC="1" .     

所以.

假设BC上存在一点G，使得平面PAG和平面PGC所成二面角的大小为60°，

设点G的坐标为（1，a，0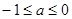），    所以

设平面PAG的法向量为，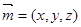

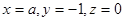则令 所以，

又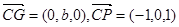设平面PCG的法向量为，

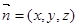则令所以 ，       

因为平面PAG和平面PGC所成二面角的大小为60°，所以

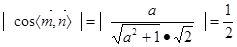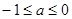  所以又所以,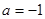 

所以线段BC上存在一点G，使得平面PAG和平面PGC所成二面角的大小为60°.

点G即为B点.

考点：直线与平面平行  二面角

点评：本题考查线面平行，考查面面角，考查学生的计算能力，正确作出面面角是关键．