题目内容
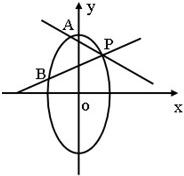 已知椭圆
已知椭圆| x2 |
| 2 |
| y2 |
| 4 |
| PF1 |
| PF2 |
(1)求P点坐标;
(2)求直线AB的斜率;
(3)求△PAB面积的最大值.
分析:(1)设出P的坐标,则可分别表示出
和
进而利用
•
=1求得x0和y0的关系,同时根据2x02+y02=4求得x0和y0即P的坐标.
(2)设出AP的方程,与椭圆方程联立根据xP=1,表示出xA和yA,同理表示出点B的坐标,进而求得AB的斜率.
(3)设出AB的方程与椭圆的方程联立,利用韦达定理表示出x1+x2和x1x2,进而求得x1-x2,最后利用弦长公式求得AB的长.利用三角形面积公式求得答案.
| PF1 |
| PF2 |
| PF1 |
| PF2 |
(2)设出AP的方程,与椭圆方程联立根据xP=1,表示出xA和yA,同理表示出点B的坐标,进而求得AB的斜率.
(3)设出AB的方程与椭圆的方程联立,利用韦达定理表示出x1+x2和x1x2,进而求得x1-x2,最后利用弦长公式求得AB的长.利用三角形面积公式求得答案.
解答:解:(1)F1(0,
),F2(0,-
),设P(x0,y0)
则
=(-x0,
-y0),
=(-x0,-
-y0)
•
=1?x02-2+y02=1?x02+y02=3
又2x02+y02=4,x0,y0>0,∴
,即所求P(1,
)
(2)设lAP:y-
=k(x-1)联立
得:(2+k2)x2-2k(k-2)x+k2-2
k-2=0
∵xP=1,∴xA=
,yA=kxA-k+
=
则A(
,
)
同理B(
,
),
∴kAB=
=
(3)设lAB:y=
x+m,联立
,
得:4x2+2
mx+m2-4=0,∴
∴|AB|=
|x1-x2|=
=
而h=
=
∴S=
|AB|•h=
•
=
≤
•
=
当且仅当m=±2时等号成立.
| 2 |
| 2 |
则
| PF1 |
| 2 |
| PF2 |
| 2 |
| PF1 |
| PF2 |
又2x02+y02=4,x0,y0>0,∴
|
| 2 |
(2)设lAP:y-
| 2 |
|
得:(2+k2)x2-2k(k-2)x+k2-2
| 2 |
∵xP=1,∴xA=
k2-2
| ||
| 2+k2 |
| 2 |
-
| ||||
| 2+k2 |
则A(
k2-2
| ||
| 2+k2 |
-
| ||||
| 2+k2 |
同理B(
k2+2
| ||
| 2+k2 |
-
| ||||
| 2+k2 |
∴kAB=
| ||||
|
| 2 |
(3)设lAB:y=
| 2 |
|
得:4x2+2
| 2 |
|
∴|AB|=
| 3 |
| 3 |
| (x1+x2)2-4x1•x2 |
| 3 |
4-
|
而h=
|
| ||||
|
| |m| | ||
|
∴S=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
4-
|
| |m| | ||
|
| ||
| 4 |
| m2(8-m2) |
| ||
| 4 |
| m2+(8-m2) |
| 2 |
| 2 |
当且仅当m=±2时等号成立.
点评:本题主要考查了直线与圆锥曲线的关系.考查了学生综合分析问题和解决问题的能力.

练习册系列答案
相关题目
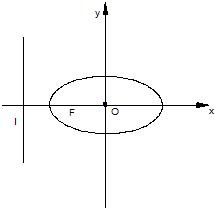 已知椭圆
已知椭圆 已知椭圆
已知椭圆