题目内容
已知函数f(x)=-x3+ax2+b,其中a,b∈R.
(1)若函数f(x)在(0,2)上单调递增,求实数a的取值范围.
(2)当x∈(0,1]时,y=f(x)图象上任意一点处的切线的倾斜角为θ,且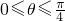 ,求a的取值范围.
,求a的取值范围.
解:(1)f′(x)=-3x2+2ax,要使f(x)在(0,2)上单调递增,
则f′(x)≥0在(0,2)上恒成立,(2分)
∵f′(x)是开口向下的抛物线,
∴ ,∴a≥3.(6分)
,∴a≥3.(6分)
(2)∵0≤θ≤ ,∴tanθ=-3x2+2ax∈[0,1].
,∴tanθ=-3x2+2ax∈[0,1].
据题意0≤-3x2+2ax≤1在(0,1]上恒成立,(9分)
由-3x2+2ax≥0,得a≥ x,a≥
x,a≥ ,(11分)
,(11分)
由-3x2+2ax≤1,得a≤ x+
x+ .
.
又 x+
x+ ≥
≥ (当且仅当x=
(当且仅当x= 时取“=”),
时取“=”),
∴a≤ (13分)
(13分)
综上,a的取值范围是 ≤a≤
≤a≤ .(14分)
.(14分)
分析:(1)求出函数的导数,利用函数f(x)在(0,2)上单调递增,f′(x)≥0恒成立,列出关系式,求实数a的取值范围.
(2)通过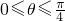 ,求出斜率的范围,即可得到导函数的值域的范围,然后求a的取值范围.
,求出斜率的范围,即可得到导函数的值域的范围,然后求a的取值范围.
点评:本题考查函数的导数求解函数的单调性以及函数的切线的斜率的范围,导数的几何意义,考查计算能力.
则f′(x)≥0在(0,2)上恒成立,(2分)
∵f′(x)是开口向下的抛物线,
∴
 ,∴a≥3.(6分)
,∴a≥3.(6分)(2)∵0≤θ≤
 ,∴tanθ=-3x2+2ax∈[0,1].
,∴tanθ=-3x2+2ax∈[0,1].据题意0≤-3x2+2ax≤1在(0,1]上恒成立,(9分)
由-3x2+2ax≥0,得a≥
 x,a≥
x,a≥ ,(11分)
,(11分)由-3x2+2ax≤1,得a≤
 x+
x+ .
.又
 x+
x+ ≥
≥ (当且仅当x=
(当且仅当x= 时取“=”),
时取“=”),∴a≤
 (13分)
(13分)综上,a的取值范围是
 ≤a≤
≤a≤ .(14分)
.(14分)分析:(1)求出函数的导数,利用函数f(x)在(0,2)上单调递增,f′(x)≥0恒成立,列出关系式,求实数a的取值范围.
(2)通过
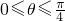 ,求出斜率的范围,即可得到导函数的值域的范围,然后求a的取值范围.
,求出斜率的范围,即可得到导函数的值域的范围,然后求a的取值范围.点评:本题考查函数的导数求解函数的单调性以及函数的切线的斜率的范围,导数的几何意义,考查计算能力.

练习册系列答案
 小题狂做系列答案
小题狂做系列答案
相关题目
已知函数f(x)=x2-bx的图象在点A(1,f(1))处的切线l与直线3x-y+2=0平行,若数列{
}的前n项和为Sn,则S2010的值为( )
| 1 |
| f(n) |
A、
| ||
B、
| ||
C、
| ||
D、
|