题目内容
已知|a|=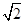 ,|b|=3,a与b夹角为45°,求使a+λb与λa+b的夹角为钝角时,λ的取值范围.
,|b|=3,a与b夹角为45°,求使a+λb与λa+b的夹角为钝角时,λ的取值范围.
【答案】
 <λ<
<λ< 且λ≠-1.
且λ≠-1.
【解析】由条件知,cos45°= ,∴a·b=3,
,∴a·b=3,
设a+λb与λa+b的夹角为θ,则θ为钝角,
∴cosθ= <0,
<0,
∴(a+λb)(λa+b)<0.
λa2+λb2+(1+λ2)a·b<0,
∴2λ+9λ+3(1+λ2)<0,∴3λ2+11λ+3<0,
∴ <λ<
<λ< .
.
若θ=180°时,a+λb与λa+b共线且方向相反,
∴存在k<0,使a+λb=k(λa+b),
∵a,b不共线,∴ ,∴k=λ=-1,
,∴k=λ=-1,
∴ <λ<
<λ< 且λ≠-1.
且λ≠-1.
本题易忽视θ=180°时,也有a·b<0,忘掉考虑夹角不是钝角而致误.

练习册系列答案
相关题目
 ,b=
,b= ,c=
,c=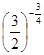 ,则a、b、c的大小关系是 ( )
,则a、b、c的大小关系是 ( )