题目内容
（24）（本小题满分10分）选修4-5，不等式选讲
已知函数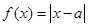
.
（Ⅰ）若不等式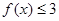
的解集为{x|－1≤x≤5}，求实数a的值；
（Ⅱ）在（Ⅰ）的条件下，若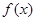
+
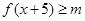对一切实数x恒成立，求实数m的取值范围.
【答案】
法一：①由
得
，解得
。
又已知不等式的解集为
，所以
，解得a=2.
②当a=2时，
，设
，
于是
所以当
时，
； 当
时，
； 当x>2时，。
综上可得，g(x)的最小值为5。
从而若
，即
对一切实数x恒成立，
则m的取值范围为（-∞，5）。………………………………10分
法二：①同法一。
②当a=2时，。设。
由
（当且仅当时等号成立），
得
的最小值为5。
从而，若，即对一切实数x恒成立。
则m的取值范围为（-∞，5）。
【解析】略
练习册系列答案
名师金手指领衔课时系列答案
相关题目
的值.
，点F1、F2为其左、右焦点，直线l的参数方程为
恒成立，记实数M的最大值是m。
的值.
，点F1、F2为其左、右焦点，直线l的参数方程为
恒成立，记实数M的最大值是m。
的参数方程为
（t为参数）,在极坐标系（与直角坐标系xoy取相同的长度单位，且以原点O为极点，以x轴正半轴为极轴）中，圆C的方程为
.
，求|PA|+|PB|.
已知三棱锥P－ABC中，PA⊥平面ABC，AB⊥AC，
，N为AB上一点，AB=4AN, M、S分别为PB,BC的中点.以A为原点，射线AB，AC，AP分别为x，y，z轴正向建立如图空间直角坐标系.
次，每次抛掷互不影响. 记正面向上的次数为奇数的概率为
，正面向上的次数为偶数的概率为
.
，试比较
的参数方程为
（t为参数）,在极坐标系（与直角坐标系xoy取相同的长度单位，且以原点O为极点，以x轴正半轴为极轴）中，圆C的方程为
.
，求|PA|+|PB|.
已知三棱锥P－ABC中，PA⊥平面ABC，AB⊥AC，
，N为AB上一点，AB=4AN, M、S分别为PB,BC的中点.以A为原点，射线AB，AC，AP分别为x，y，z轴正向建立如图空间直角坐标系.
次，每次抛掷互不影响. 记正面向上的次数为奇数的概率为
，正面向上的次数为偶数的概率为
.
，试比较