题目内容
(本小题满分12分)
已知函数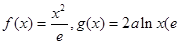 为自然对数的底数).
为自然对数的底数).
(Ⅰ)求F(x)=f(x) g(x)的单调区间,若F(x)有最值,请求出最值;
g(x)的单调区间,若F(x)有最值,请求出最值;
(Ⅱ)是否存在正常数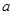 ,使f(x)与g(x)的图象有且只有一个公共点,且在该公共点处有共同的切线?若存在,求出
,使f(x)与g(x)的图象有且只有一个公共点,且在该公共点处有共同的切线?若存在,求出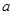 的值,以及公共点坐标和公切线方程;若不存在,请说明理由.
的值,以及公共点坐标和公切线方程;若不存在,请说明理由.
(Ⅰ)所以当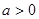 时,
时, 的单调递减区间为
的单调递减区间为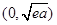 ,单调递增区间为
,单调递增区间为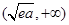 ,最小值为
,最小值为 ,无最大值
;
,无最大值
;
(Ⅱ)存在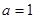 ,使
,使 的图象有且只有一个公共点,且在该公共点处有共同的切线,易求得公共点坐标为
的图象有且只有一个公共点,且在该公共点处有共同的切线,易求得公共点坐标为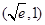 ,公切线方程为
,公切线方程为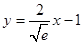 。
。
【解析】(1)求F(x)=f(x)-g(x)的单调区间,及函数F(x)的最值,考虑到先列出函数的表达式,再根据表达式求出导函数F′(x),根据导函数在区间的正负性判断函数的单调区间,再使导函数等于0求出函数的极值,即可得到答案.
(2)若f(x)与g(x)的图象有且只有一个公共点,则方程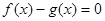 有且只有一解,所以函数F(x)有且只有一个零点,由(Ⅰ)的结论可知
有且只有一解,所以函数F(x)有且只有一个零点,由(Ⅰ)的结论可知 .当a=1时,求f(x)与g(x)的一个公共点,并求它们在该公共点处的切线方程,故根据(1)可判断方程F(x)=f(x)-g(x)有最小值0,故此点即为f(x)与g(x)的一个公共点.再根据导函数求出公共点处切线.即可根据直线方程的求法求出切线方程.
.当a=1时,求f(x)与g(x)的一个公共点,并求它们在该公共点处的切线方程,故根据(1)可判断方程F(x)=f(x)-g(x)有最小值0,故此点即为f(x)与g(x)的一个公共点.再根据导函数求出公共点处切线.即可根据直线方程的求法求出切线方程.
(Ⅰ) ………… 1分
………… 1分
①当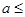 0时,
0时, 恒成立,F(x)在(0,+
恒成立,F(x)在(0,+ )上是增函数,F(x)只有一个单调递增区间(0,+
)上是增函数,F(x)只有一个单调递增区间(0,+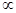 ),没有最值.…………2分
),没有最值.…………2分
②当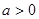 时,
时,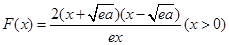 ,
,
若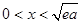 ,则
,则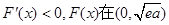 上单调递减;
上单调递减;
若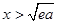 ,则
,则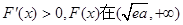 上单调递增,
上单调递增,
∴当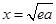 时,
时, 有极小值,也是最小值,
有极小值,也是最小值,
即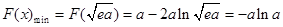 ………… 5分
………… 5分
所以当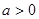 时,
时, 的单调递减区间为
的单调递减区间为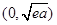
单调递增区间为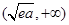 ,最小值为
,最小值为 ,无最大值
………… 6分
,无最大值
………… 6分
(Ⅱ)方法一,若f(x)与g(x)的图象有且只有一个公共点,
则方程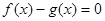 有且只有一解,所以函数F(x)有且只有一个零点 …… 7分
有且只有一解,所以函数F(x)有且只有一个零点 …… 7分
由(Ⅰ)的结论可知 ………… 8分
………… 8分
此时,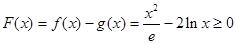 ,
,
∴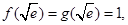 ∴f(x)与g(x)的图象的唯一公共点坐标为
∴f(x)与g(x)的图象的唯一公共点坐标为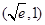
又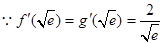 ,∴f(x)与g(x)的图象在点
,∴f(x)与g(x)的图象在点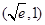 处有共同的切线,
处有共同的切线,
其方程为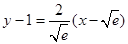 ,即
,即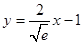 ………… 12分
………… 12分
综上所述,存在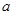
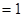 ,使
,使 的图象有且只有一个公共点
的图象有且只有一个公共点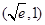 ,且在该点处的公切线方程为
,且在该点处的公切线方程为 ………… 14分
………… 14分
方法二:设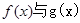 图象的公共点坐标为
图象的公共点坐标为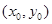 ,
,
|
 ,即
,即
由②得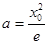 ,代入①得
,代入①得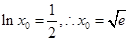 ,从而
,从而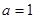 ………… 8分
………… 8分
此时由(1)可知 ,∴
,∴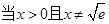 时,
时,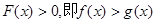
因此除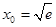 外,再没有其它
外,再没有其它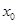 ,使
,使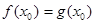 ………… 11分
………… 11分
故存在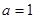 ,使
,使 的图象有且只有一个公共点,且在该公共点处有共同的切线,易求得公共点坐标为
的图象有且只有一个公共点,且在该公共点处有共同的切线,易求得公共点坐标为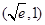 ,公切线方程为
,公切线方程为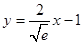 ………… 12分
………… 12分

 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案