Question

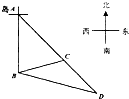（2013•宁德模拟）岛A观察站发现在其东南方向有一艘可疑船只，正以每小时10海里的速度向东南方向 航行（如图所示），观察站即刻通知在岛A正南方向B处巡航的海监船前往检查．接到 通知后，海监船测得可疑船只在其北偏东75°方向且相距10海里的C处，随即以每小时10

3

海里的速度前往拦截．
（I）问：海监船接到通知时，距离岛A多少海里？
（II）假设海监船在D处恰好追上可疑船只，求它的航行方向及其航行的时间．

Answer 1

分析：（I）在△ABC中，依题意，利用正弦定理即可求得AB；
（II）在△BCD中，利用余弦定理可求得航行的方向及时间；

解答：解：（I）依题意得∠BAC=45°，∠ABC=75°，BC=10，
∴∠ACB=60°，…2分
在△ABC中，由正弦定理得：

AB

sin∠ACB

=

BC

sin∠BAC

…3分
∴AB=

BCsin∠ACB

sin∠BAC

=

10sin60°

sin45°

=

10× 3 2

2 2

=5

6

．
答：海监船接到通知时，距离岛A5

6

海里…5分
（II）设海监船航行时间为t小时，
则BD=10

3

t，CD=10t，…6分
又∵∠BCD=180°-∠ACB=180°-60°=120°，
∴BD²=BC²+CD²-2BC•CDcos120°，…7分
∴300t²=100+100t²-2×10×10t•（-

1

2

），
∴2t²+t-1=0，
解得t=1或t=-

1

2

（舍去）…9分
∴CD=10，
∴BC=CD，
∴∠CBD=

1

2

（180°-120°）=30°，
∴∠ABD=75°+30°=105°，…11分
答：海监船的方位角105°航行，航行时间为1个小时…12分

点评：本题主要考查正、余弦定理，解三角形等基础知识，考查抽象概括能力、运算求解能力以及应用意识，考查函数方程思想，属于难题．