题目内容
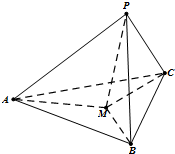
 如图,在三棱锥P-ABC中,底面△ABC为等边三角形,∠APC=90°,PB=AC=2PA=4,O为AC的中点.
如图,在三棱锥P-ABC中,底面△ABC为等边三角形,∠APC=90°,PB=AC=2PA=4,O为AC的中点.(Ⅰ)求证:BO⊥PA;
(Ⅱ)判断在线段AC上是否存在点Q(与点O不重合),使得△PQB为直角三角形?若存在,试找出一个点Q,并求
| AQ | QC |
分析:对(I),先通过证线线垂直,证线面垂直,再由线面垂直证线线垂直.
对(II),在(I)基础上可知平面ABC与平面PAC的垂直性,所以只需过P作交线AC的垂线,由线线垂直⇒线面垂直,再由线面垂直⇒线线垂直,证明直角三角形的存在性.在上述条件下求出
的值即可.
对(II),在(I)基础上可知平面ABC与平面PAC的垂直性,所以只需过P作交线AC的垂线,由线线垂直⇒线面垂直,再由线面垂直⇒线线垂直,证明直角三角形的存在性.在上述条件下求出
| AQ |
| QC |
解答: 解:(Ⅰ)证明:如图,连接PO,
解:(Ⅰ)证明:如图,连接PO,
在等边△ABC中,∵O是AC的中点,且AC=4,
∴BO⊥AC,BO=2
.
在直角△PAC中,因为O是斜边AC的中点,且AC=4,∴PO=2,
在△PBO中,由PB=4,得PB2=PO2+BO2,
∴PO⊥BO
又∵AC∩PO=O,AC?平面PAC,PO?平面PAC,
∴BO⊥平面PAC,(5分)
又∵PA?平面PAC,
∴BO⊥PA. (7分)
(Ⅱ)线段AC上存在点Q,使得△PQB为直角三角形.
如图,过P作PM⊥AC于点M,连接BM,
∵BO⊥平面PAC,
∴BO⊥PM.
又∵BO∩AC=O,BO?平面ABC,AC?平面ABC,
∴PM⊥平面ABC,(10分)
∴PM⊥BM,即△PMB为直角三角形.
故当点Q与点M重合时,△PQB为直角三角形. (12分)
在直角△PAC中,由∠APC=90°,AC=2PA=4,PO=2,
得AM=1,(即AQ=1),MC=3(即QC=3),
∴当
=
(即
=
)时,△PQB为直角三角形. (14分)
 解:(Ⅰ)证明:如图,连接PO,
解:(Ⅰ)证明:如图,连接PO,在等边△ABC中,∵O是AC的中点,且AC=4,
∴BO⊥AC,BO=2
| 3 |
在直角△PAC中,因为O是斜边AC的中点,且AC=4,∴PO=2,
在△PBO中,由PB=4,得PB2=PO2+BO2,
∴PO⊥BO
又∵AC∩PO=O,AC?平面PAC,PO?平面PAC,
∴BO⊥平面PAC,(5分)
又∵PA?平面PAC,
∴BO⊥PA. (7分)
(Ⅱ)线段AC上存在点Q,使得△PQB为直角三角形.
如图,过P作PM⊥AC于点M,连接BM,
∵BO⊥平面PAC,
∴BO⊥PM.
又∵BO∩AC=O,BO?平面ABC,AC?平面ABC,
∴PM⊥平面ABC,(10分)
∴PM⊥BM,即△PMB为直角三角形.
故当点Q与点M重合时,△PQB为直角三角形. (12分)
在直角△PAC中,由∠APC=90°,AC=2PA=4,PO=2,
得AM=1,(即AQ=1),MC=3(即QC=3),
∴当
| AQ |
| QC |
| 1 |
| 3 |
| AM |
| MC |
| 1 |
| 3 |
点评:本题主要考查线面垂直的判定与线面垂直的性质.即线线垂直?线面垂直的相互转化.
勾股定理是平面几何中证明线线垂直的重要方法.
勾股定理是平面几何中证明线线垂直的重要方法.

练习册系列答案
相关题目
 如图,在三棱锥P-ABC中,PA、PB、PC两两垂直,且PA=3.PB=2,PC=1.设M是底面ABC内一点,定义f(M)=(m,n,p),其中m、n、p分别是三棱锥M-PAB、三棱锥M-PBC、三棱锥M-PCA的体积.若f(M)=(
如图,在三棱锥P-ABC中,PA、PB、PC两两垂直,且PA=3.PB=2,PC=1.设M是底面ABC内一点,定义f(M)=(m,n,p),其中m、n、p分别是三棱锥M-PAB、三棱锥M-PBC、三棱锥M-PCA的体积.若f(M)=( 如图,在三棱锥P-ABC中,PA⊥底面ABC,∠ACB=90°,AE⊥PB于E,AF⊥PC于F,若PA=AB=2,∠BPC=θ,则当△AEF的面积最大时,tanθ的值为( )
如图,在三棱锥P-ABC中,PA⊥底面ABC,∠ACB=90°,AE⊥PB于E,AF⊥PC于F,若PA=AB=2,∠BPC=θ,则当△AEF的面积最大时,tanθ的值为( ) 如图,在三棱锥P-ABC中,PA=PB=AB=2,BC=3,∠ABC=90°,平面PAB⊥平面ABC,D、E分别为AB、AC中点.
如图,在三棱锥P-ABC中,PA=PB=AB=2,BC=3,∠ABC=90°,平面PAB⊥平面ABC,D、E分别为AB、AC中点. 如图,在三棱锥P-ABC中,已知PA=PB=PC,∠BPA=∠BPC=∠CPA=40°,一绳子从A点绕三棱锥侧面一圈回到点A的最短距离是
如图,在三棱锥P-ABC中,已知PA=PB=PC,∠BPA=∠BPC=∠CPA=40°,一绳子从A点绕三棱锥侧面一圈回到点A的最短距离是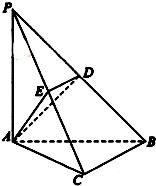 如图,在三棱锥P-ABC中,PA⊥底面ABC,∠BCA=90°,AP=AC,点D,E分别在棱
如图,在三棱锥P-ABC中,PA⊥底面ABC,∠BCA=90°,AP=AC,点D,E分别在棱