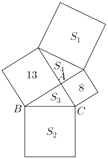
题目内容
【题目】已知一列函数![]() ,设直线
,设直线![]() 与
与![]() 的交点为
的交点为![]() ,点
,点![]() 在
在![]() 轴和直线
轴和直线![]() 上的射影分别为
上的射影分别为![]() ,记
,记![]() 的面积为
的面积为![]() ,
,![]() 的面积为
的面积为![]() .
.
(1)求![]() 的最小值,并指出此时
的最小值,并指出此时![]() 的取值;
的取值;
(2)在![]() 中任取一个函数,求该函数在
中任取一个函数,求该函数在![]() 上是增函数或在
上是增函数或在![]() 上是减函数的概率;
上是减函数的概率;
(3)是否存在正整数![]() ,使得
,使得![]() 成立,若存在,求出
成立,若存在,求出![]() 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
【答案】(1)![]() ,
,![]() (2)
(2)![]() (3)不存在
(3)不存在
【解析】
(1)根据题意表示出![]() ,结合基本不等式即可求得最小值及取得最小值时
,结合基本不等式即可求得最小值及取得最小值时![]() 的值.
的值.
(2)根据函数表达式,结合打勾函数的图像与性质,即可判断在![]() 上是增函数或在
上是增函数或在![]() 上是减函数的所有情况,即可求得在
上是减函数的所有情况,即可求得在![]() 中满足条件的概率.
中满足条件的概率.
(3)由直线![]() 与
与![]() 的交点为
的交点为![]() ,即可求得点
,即可求得点![]() 的坐标.由点
的坐标.由点![]() 在
在![]() 轴和直线
轴和直线![]() 上的射影分别为
上的射影分别为![]() ,结合点到直线距离公式即可求得
,结合点到直线距离公式即可求得![]() 的坐标.表示出
的坐标.表示出![]() 的面积
的面积![]() ,
,![]() 的面积
的面积![]() .将、
.将、![]() 的表达式代入等式
的表达式代入等式![]() 中,通过化简变形,检验即可得知
中,通过化简变形,检验即可得知![]() 的值,若不存在.
的值,若不存在.
(1)函数![]()
所以![]()
由基本不等式可知, ![]()
当且仅当![]() 时取等号,即
时取等号,即![]() 时取等号
时取等号
所以![]() 的最小值为
的最小值为![]() ,当
,当![]() 时取等号
时取等号
(2)因为![]() 结合对勾函数的图像与性质
结合对勾函数的图像与性质
所以![]()
![]()
![]()
![]()
在![]() 内满足单调递增,而
内满足单调递增,而![]() 不满足.因而满足在
不满足.因而满足在![]() 内满足单调递增的函数共有49个.
内满足单调递增的函数共有49个.
因为![]() ,而
,而![]()
而![]()
![]()
![]() 满足在
满足在![]() 内单调递减,所以此时共有
内单调递减,所以此时共有![]()
所以该函数在![]() 上是增函数或在
上是增函数或在![]() 上是减函数的个数共有
上是减函数的个数共有![]() 个
个
即该函数在![]() 上是增函数或在
上是增函数或在![]() 上是减函数的概率为
上是减函数的概率为![]()
(3)因为直线![]() 与
与![]() 的交点为
的交点为![]()
所以![]()
点![]() 在
在![]() 轴上的射影为
轴上的射影为![]() ,所以
,所以![]()
点![]() 在直线
在直线![]() 上的射影为
上的射影为![]() ,直线方程化为一般式可得
,直线方程化为一般式可得![]()
则由点到直线距离公式可得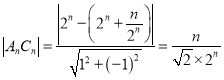
从![]() 向
向![]() 轴作垂直,交
轴作垂直,交![]() 于点E
于点E
则![]()
所以![]()
![]()
画出函数图像如下图所示:
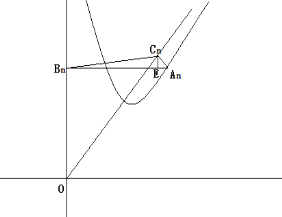
所以![]() 的面积为
的面积为![]()
![]() 的面积为
的面积为![]()
![]()
假设存在正整数![]() ,使得
,使得![]() 成立,代入可得
成立,代入可得
![]()
将式子化简可得![]()
当![]() 时,等式左边等于20,等式右边等于17,等式不成立
时,等式左边等于20,等式右边等于17,等式不成立
当![]() 时,等式左边等于32,等式右边等于68,等式不成立
时,等式左边等于32,等式右边等于68,等式不成立
当![]() 时,等式左边小于0,等式右边大于0,等式不成立.
时,等式左边小于0,等式右边大于0,等式不成立.
综上可知,不存在正整数![]() ,使得
,使得![]() 成立
成立

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目