题目内容

已知在△ABC中，∠ACB=90°，BC=4，AC=3，P是AB上一点，则点P到AC，BC的距离乘积的最大值是（　　）
A、2B、3C、4D、5
分析：设点P到AC，BC的距离分别是x和y，最上方小三角形和最大的那个三角形相似，它们对应的边有此比例关系，进而求得x和y的关系式，进而表示出xy的表达式，利用二次函数的性质求得xy的最大值．
解答：解：如图，设点P到AC，BC的距离分别是x和y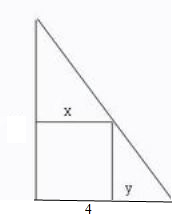，精英家教网
最上方小三角形和最大的那个三角形相似，
它们对应的边有此比例关系，即
x
3
=
4-y
4
4，
所以4x=12-3y，y=
12-4x
3
，求xy最大，也就是那个矩形面积最大．
xy=x•
12-4x
3
=-
4
3
•（x2-3x），
∴当x=
3
2
时，xy有最大值3
故选B．
点评：本题主要考查了三角函数的几何计算．解题的关键是通过题意建立数学模型，利用二次函数的性质求得问题的答案．
练习册系列答案
相关题目
已知在△ABC中，点A、B的坐标分别为（-2，0）和（2，0），点C在x轴上方．
（Ⅰ）若点C的坐标为（2，3），求以A、B为焦点且经过点C的椭圆的方程；
（Ⅱ）若∠ACB=45°，求△ABC的外接圆的方程；
（Ⅲ）若在给定直线y=x+t上任取一点P，从点P向（Ⅱ）中圆引一条切线，切点为Q．问是否存在一个定点M，恒有PM=PQ？请说明理由．
已知在△ABC中，角A、B、C所对的边分别为a、b、c；且a=3
3
，c=2，B=150°，求边b的长和S△ABC．
已知
a
=（sinx，
3
4
），
b
=（cos（x+
π
3
），1）函数f（x）=
a
•
b
．
（1）求f（x）的最值和单调递减区间；
（2）已知在△ABC中，角A、B、C的对边分别为a，b，c，f（A）=0，a=
3
，求△ABC的面积的最大值．
已知在△ABC中，内角A，B，C所对的边分别为a，b，c，且acosC+
3
2
c=b．
（Ⅰ）求角A；
（Ⅱ）若a=l，且
3
c-2b=1，求角B．
（2010•泸州二模）已知在△ABC中，角A、B、C的对边分别是a、b、c，且tanB=
2-
3
a2+c2-b2
，
BC
•
BA
=
1
2
．
（Ⅰ）求tanB的值；
（Ⅱ）求
2sin2
B
2
+2sin
B
2
cos
B
2
-1
cos(
π
4
-B)
的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网