Question

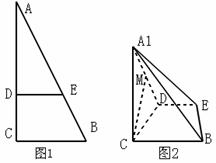
（2012年高考（上海理））如图,AD与BC是四面体ABCD中互相垂直的棱,BC=2。若AD=2c,且AB+BD=AC+CD=2a,其中a、c为常数,则四面体ABCD的体积的最大值是 _________ .

Answer 1

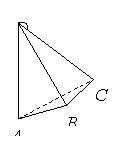
作BE⊥AD于E,连接CE,则AD⊥平面BEC,所以CE⊥AD,

由题设,B与C都是在以AD为焦距的椭球上,且BE、CE都

垂直于焦距AD,所以BE=CE.  取BC中点F,

连接EF,则EF⊥BC,EF=2,,

四面体ABCD的体积,显然,当E在AD中点,即 B是短轴端点时,BE有最大值为b=,所以.

 

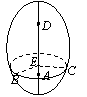
【评注】 本题把椭圆拓展到空间,对缺少联想思维的考生打击甚大!当然,作为填空押轴题,区分度还是要的,不过,就抢分而言,胆大、灵活的考生也容易找到突破点:AB=BD(同时AC=CD),从而致命一击,逃出生天!