题目内容
(本小题满分12分)
正三棱柱ABC—A1B1C1中，已知A1A = AB，D为C1C的中点，O为A1B与AB1的交点．
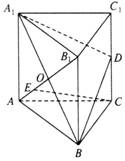求二面角A—A1B—D的大小．
若点E为AO的中点，求证：EC∥平面A1BD；
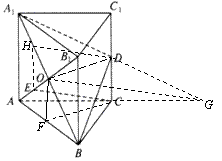
(1) 解：（法一）取AB中点F，连结OD、CF
∵ O为A1B中点
∴ OF∥AA1
∴ OF
CD
∴ 四边形OFCD为平行四边形
∴ OD∥FC
∵ △ABC为等边三角形，F为AB中点
∴ CF⊥AB
而AA1⊥平面ABC
∴ AA1⊥CF
∴ CF⊥平面ABA1
∴ OD⊥平面ABA1
∵ OD
平面A1BD
∴ 平面A1BD⊥平面A1AB
∴ 二面角A—A1B—D的大小为90
6分
（法二）连结OD、AD
∵ DA1 = DB，O为A1B中点，
∴ DO⊥A1B
∵ A1A = AB，
∴ AO⊥A1B
∴ ∠AOD为二面角A—A1B—D的平面角
设AA1 = 2，则
而
∴ 
∴ 
∴二面角A—A1B—D的大小为90
(2) 证明：（法一）延长A1D、AC交于G，连结OG
∵ CD
AA1 ∴ C为AG中点
∵ E为AO中点 ∴ EC∥OG
∵ OG平面A1BD
∴ EC∥平面A1BD 12分
（法二）取A1O中点H
∵ E为OA中点
∴ EHAA1 ∴ EHCD
∴ EHDC为平行四边形 ∴ EC∥FD
∵ FD平面A1BD
∴ EC∥平面A1BD
练习册系列答案
新思维寒假作业系列答案
相关题目
，且
。①求
的最大值及最小值；②求
、
、
.现有3名工人独立地从中任选一个项目参与建设.求：
