题目内容
(本题满分9分)
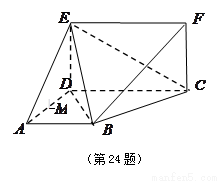
如图所示的多面体中,已知直角梯形 和矩形
和矩形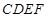 所在的平面互相垂直,
所在的平面互相垂直,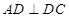 ,
,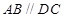 ,
,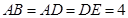 ,
,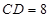 .
.
(Ⅰ)证明: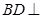 平面
平面 ;
;
(Ⅱ)设二面角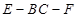 的平面角为
的平面角为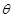 ,求
,求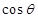 的值;
的值;
(Ⅲ)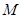 为
为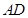 的中点,在
的中点,在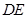 上是否存在一点
上是否存在一点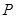 ,使得
,使得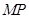 ∥平面
∥平面 ?若存在,求出
?若存在,求出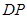 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
【答案】
(Ⅰ)证明:以 分别为
分别为 轴建立空间直角坐标系, 则
轴建立空间直角坐标系, 则 ,
,
 ∵
∵ ,
,
 ,
,
∴ ,且
,且 与
与 相交于
相交于 ,
,
∴ 平面
平面 .……………………………3分
.……………………………3分
(Ⅱ)∵ 平面
平面 ,
,  是平面
是平面 的一个法向量
的一个法向量 ,
,
设 平面
平面 的一个法向量,
的一个法向量,
则

 取
取 =(1,1,2),
=(1,1,2),
则cosθ= =
= =
= .
…………………………………6分
.
…………………………………6分
(Ⅲ)∵ ,设
,设 ,
, 为
为 上一点,则
上一点,则 ,
,
∵ ∥平面
∥平面 ,
,
∴ ⊥
⊥



 .
.
∴当 时,
时, ∥平面
∥平面 . …………………………………………9分
. …………………………………………9分
【解析】略

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 对一切实数
对一切实数 都有
都有
 成立,且
成立,且 .(1)求
.(1)求 的值 (2)求
的值 (2)求 ,设P:当
,设P:当 时,不等式
时,不等式 恒成立;Q:当
恒成立;Q:当 时,
时, 是单调函数。如果满足P成立的
是单调函数。如果满足P成立的 的集合记为
的集合记为 ,满足Q成立的
,满足Q成立的
 ,求
,求 (
( 为全集)
为全集) 轴上的抛物线过点
轴上的抛物线过点 .
. 作直线交抛物线于
作直线交抛物线于 两点,使得
两点,使得 恰好平分线段
恰好平分线段 ,求直线
,求直线 的定义域为集合
的定义域为集合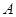 ,
, .
. ,求实数a的取值范围;
,求实数a的取值范围; ,a=
,a= ,求
,求 及
及 .
.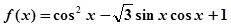 .
.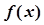 的单调递增区间;
的单调递增区间;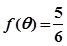 ,
,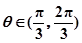 ,求
,求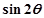 的值;
的值;  中,已知直线
中,已知直线 被圆
被圆 截得的弦长为
截得的弦长为 .
. 的方程;
的方程; 轴相交于
轴相交于 ,
, ,
, 轴于
轴于 ,
, 两点.当点
两点.当点 为直径的圆
为直径的圆 是否经过圆
是否经过圆 的顶点
的顶点 上,
上, ,
, 过圆心
过圆心 ,求点
,求点