题目内容
已知E、E1分别是正方体ABCD—A1B
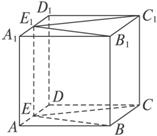
证明:如下图,连结EE1.
∵E1、E分别为A1D1、AD中点,
∴A1E1![]() AE.
AE.
∴A1E1EA为平行四边形.
∴A![]() E1E.
E1E.
又∵A![]() B1B,
B1B,
∴E1E![]() B1B.
B1B.
∴四边形E1EBB1是平行四边形.
∴E1B1∥EB.同理,E
又∠B1E
∴∠B1E

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
题目内容
已知E、E1分别是正方体ABCD—A1B
证明:如下图,连结EE1.
∵E1、E分别为A1D1、AD中点,

∴A1E1![]() AE.
AE.
∴A1E1EA为平行四边形.
∴A![]() E1E.
E1E.
又∵A![]() B1B,
B1B,
∴E1E![]() B1B.
B1B.
∴四边形E1EBB1是平行四边形.
∴E1B1∥EB.同理,E
又∠B1E
∴∠B1E

 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案