题目内容
双曲线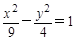 与直线
与直线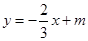 (
(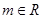 )的公共点的个数为( ).
)的公共点的个数为( ).
| A.0 | B.1 | C.0或1 | D.0或1或2 |
C
解析试题分析:双曲线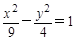 的渐近线方程为
的渐近线方程为 ,所以如果
,所以如果 ,直线
,直线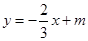 与渐近线平行,与双曲线没有交点;如果
与渐近线平行,与双曲线没有交点;如果 ,直线
,直线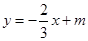 与双曲线的左支或右支有一个交点,所以双曲线
与双曲线的左支或右支有一个交点,所以双曲线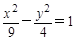 与直线
与直线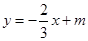 (
(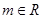 )的公共点的个数为0或1.
)的公共点的个数为0或1.
考点:本小题主要考查双曲线的渐近线、直线与双曲线的位置关系,考查学生数形结合思想的应用.
点评:双曲线的渐近线在研究直线与双曲线的位置关系时是不可忽略的内容,而且双曲线是不封闭的曲线,直线与双曲线只有一个交点,并不能说明直线与双曲线相切,要结合图象进行判断.

练习册系列答案
相关题目
已知曲线C:  与抛物线
与抛物线 的一个交点为M,
的一个交点为M, 为抛物线的焦点,若
为抛物线的焦点,若 ,则b的值为
,则b的值为
A. | B.- | C. | D.- |
若抛物线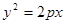 的焦点与椭圆
的焦点与椭圆 的右焦点重合,则
的右焦点重合,则 的值为
的值为
| A.-2 | B.2 | C.-4 | D.4 |
若焦点在 轴上的椭圆
轴上的椭圆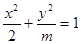 的离心率为
的离心率为 ,则
,则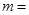 ( )
( )
A.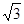 | B.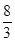 | C.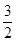 | D.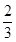 |
 为抛物线
为抛物线 的焦点,
的焦点, 为抛物线上三点.
为抛物线上三点. 为坐标原点,若
为坐标原点,若 是
是 的重心,
的重心, 的面积分别为
的面积分别为 3,则
3,则 +
+ +
+ 的值为: ( )
的值为: ( )
| A.3 | B.4 | C.6 | D.9 |
设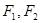 是椭圆
是椭圆 的两个焦点,
的两个焦点,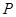 是椭圆上的点,且
是椭圆上的点,且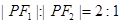 ,则
,则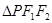 的面积为( )
的面积为( )
| A.4 | B.6 | C.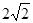 | D.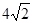 |
已知点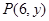 在抛物线
在抛物线 上,
上, 为抛物线焦点, 若
为抛物线焦点, 若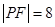 , 则点
, 则点 到抛物线准线的距离等于( )
到抛物线准线的距离等于( )
| A.2 | B.1 | C.4 | D.8 |
已知双曲线 的一个焦点与抛物线
的一个焦点与抛物线
的焦点重合,且双曲线的离心率等于 ,则该双曲线的标准方程为( )
,则该双曲线的标准方程为( )
A. | B. |
C. | D. |
设定点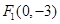 、
、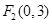 ,动点
,动点 满足条件
满足条件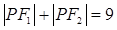 ,则点
,则点 的轨迹是( )
的轨迹是( )
| A.椭圆 | B.线段 | C.不存在 | D.线段或椭圆 |