题目内容
椭圆过点(3,0),离心率e= ,求椭圆的标准方程.
,求椭圆的标准方程.
解:当椭圆的焦点在x轴上时,∵a=3, =
= ,
,
∴c= ,
,
∴b2=a2-c2=3.
∴椭圆方程为 =1.
=1.
当椭圆的焦点在y轴上时,∵b=3, =
= ,
,
∴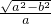 =
= ,解得a2=27.
,解得a2=27.
故椭圆的方程为 =1.
=1.
综上知,所求椭圆的方程为 =1,或
=1,或  =1.
=1.
分析:由于椭圆的焦点位置未定,故需要进行分类讨论,进而可求椭圆的标准方程.
点评:本题重点考查椭圆的标准方程,考查分类讨论的数学思想,属于基础题.
 =
= ,
,∴c=
 ,
,∴b2=a2-c2=3.
∴椭圆方程为
 =1.
=1.当椭圆的焦点在y轴上时,∵b=3,
 =
= ,
,∴
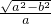 =
= ,解得a2=27.
,解得a2=27.故椭圆的方程为
 =1.
=1.综上知,所求椭圆的方程为
 =1,或
=1,或  =1.
=1.分析:由于椭圆的焦点位置未定,故需要进行分类讨论,进而可求椭圆的标准方程.
点评:本题重点考查椭圆的标准方程,考查分类讨论的数学思想,属于基础题.

练习册系列答案
相关题目