题目内容
用数学归纳法证明:如果{an}是一个等差数列,那么an=a1+(n-1)d对一切n∈N*都成立.
思路分析:我们知道等差、等比数列的通项公式都是通过递推得出结论的,无法用演绎法证明它们的无穷性,数学归纳法以一次逻辑的推理代替了无限的验证过程.
证明:(1)当n=1时,左=a1,
右=a1+(1-1)d=a1,所以等式成立.
(2)假设当n=k(k∈N)时等式成立,即ak=a1+(k-1)d.
那么ak+1=ak+d=a1+(k-1)d+d=a1+[(k+1)-1]d.
∴当n=k+1时,等式成立,由(1)(2)知对任何n∈N*等式成立.
方法归纳
因为数列的通项公式,前n项和公式都是关于自然数n的函数,所以在关于这类问题的证明上,如果我们无法确定其他比较简便的证明方法,那么数学归纳法是证明它们的一种有效方法.

练习册系列答案
相关题目
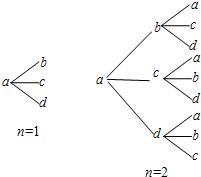 用a,b,c,d四个不同字母组成一个含n+1(n∈N+)个字母的字符串,要求由a开始,相邻两个字母不同.例如n=1时,排出的字符串是ab,ac,ad;n=2时排出的字符串是aba,abc,abd,aca,acb,acd,ada,adb,adc,…,如图所示.记这含n+1个字母的所有字符串中,排在最后一个的字母仍是a的字符串的种数为an.
用a,b,c,d四个不同字母组成一个含n+1(n∈N+)个字母的字符串,要求由a开始,相邻两个字母不同.例如n=1时,排出的字符串是ab,ac,ad;n=2时排出的字符串是aba,abc,abd,aca,acb,acd,ada,adb,adc,…,如图所示.记这含n+1个字母的所有字符串中,排在最后一个的字母仍是a的字符串的种数为an.
 ;
; .
.
 ;
; .
.