题目内容
已知正方形ABCD的边长为1,点E是AB边上的动点,则(Ⅰ)
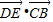 的值为 ;
的值为 ;(Ⅱ)
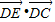 的最大值为 .
的最大值为 .
【答案】分析:(Ⅰ)以AB、AD所在直线为x轴、y轴,建立坐标系如图,可得出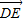 =(x,-1),
=(x,-1),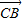 =(0,-1),再用向量数量积的坐标运算公式,可算出
=(0,-1),再用向量数量积的坐标运算公式,可算出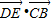 的值;
的值;
(II)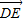 =(x,-1),
=(x,-1),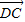 =(1,0),由向量数量积的坐标运算公式,得
=(1,0),由向量数量积的坐标运算公式,得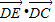 =x,结合点E在线段AB上运动,可得到x的最大值为1,即为所求的最大值.
=x,结合点E在线段AB上运动,可得到x的最大值为1,即为所求的最大值.
解答:解:以AB、AD所在直线为x轴、y轴,建立坐标系如图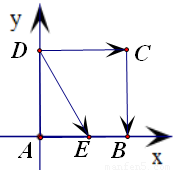
可得A(0,0),B(1,0),C(1,1),D(0,1)
设E(x,0),其中0≤x≤1
(Ⅰ)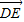 =
=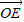 -
-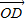 =(x,-1),
=(x,-1),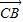 =
=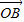 -
-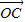 =(0,-1)
=(0,-1)
∴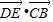 =x•0+(-1)•(-1)=1;
=x•0+(-1)•(-1)=1;
(Ⅱ)∵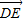 =(x,-1),
=(x,-1),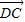 =
=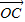 -
-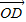 =(1,0)
=(1,0)
∴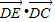 =x•1+(-1)•0=x
=x•1+(-1)•0=x
∵点E是AB边上的动点,即0≤x≤1
∴x的最大值为1,即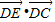 的最大值为1
的最大值为1
点评:本题在正方形中,求向量数量积的最大值,着重考查了平面向量数量积的定义及其坐标运算公式等知识,属于基础题.
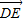 =(x,-1),
=(x,-1),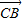 =(0,-1),再用向量数量积的坐标运算公式,可算出
=(0,-1),再用向量数量积的坐标运算公式,可算出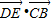 的值;
的值;(II)
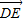 =(x,-1),
=(x,-1),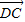 =(1,0),由向量数量积的坐标运算公式,得
=(1,0),由向量数量积的坐标运算公式,得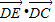 =x,结合点E在线段AB上运动,可得到x的最大值为1,即为所求的最大值.
=x,结合点E在线段AB上运动,可得到x的最大值为1,即为所求的最大值.解答:解:以AB、AD所在直线为x轴、y轴,建立坐标系如图

可得A(0,0),B(1,0),C(1,1),D(0,1)
设E(x,0),其中0≤x≤1
(Ⅰ)
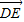 =
=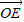 -
-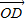 =(x,-1),
=(x,-1),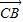 =
=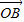 -
-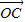 =(0,-1)
=(0,-1)∴
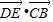 =x•0+(-1)•(-1)=1;
=x•0+(-1)•(-1)=1;(Ⅱ)∵
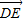 =(x,-1),
=(x,-1),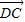 =
=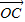 -
-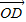 =(1,0)
=(1,0)∴
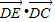 =x•1+(-1)•0=x
=x•1+(-1)•0=x∵点E是AB边上的动点,即0≤x≤1
∴x的最大值为1,即
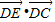 的最大值为1
的最大值为1点评:本题在正方形中,求向量数量积的最大值,着重考查了平面向量数量积的定义及其坐标运算公式等知识,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知正方形ABCD的边长为1,设
=
,
=
,
=
,则|
-
+
|等于( )
| AB |
| a |
| BC |
| b |
| AC |
| c |
| a |
| b |
| c |
| A、0 | ||
B、
| ||
| C、2 | ||
D、2
|
 已知正方形ABCD的边长为2,中心为O,四边形PACE是直角梯形,设PA⊥平面ABCD,且PA=2,CE=1,
已知正方形ABCD的边长为2,中心为O,四边形PACE是直角梯形,设PA⊥平面ABCD,且PA=2,CE=1, 如图,已知正方形ABCD的中心为E(-1,0),一边AB所在的直线方程为x+3y-5=0,求其它三边所在的直线方程.
如图,已知正方形ABCD的中心为E(-1,0),一边AB所在的直线方程为x+3y-5=0,求其它三边所在的直线方程.