题目内容
(本小题满分14分)已知椭圆 过点
过点 ,离心率
,离心率 ,
, 为椭圆
为椭圆 上的一点,
上的一点, 为抛物线
为抛物线 上一点,且
上一点,且 为线段
为线段 的中点.
的中点.
(1)求椭圆 的方程;
的方程;
(2)求直线 的方程.
的方程.
(1) ;(2)
;(2) .
.
【解析】
试题分析:(1)将 代入椭圆方程,结合
代入椭圆方程,结合 得到关于
得到关于 的方程组,解得
的方程组,解得 ,即得椭圆方程;(2)设
,即得椭圆方程;(2)设 点坐标为
点坐标为 ,则
,则 点坐标为
点坐标为 ,分别代入椭圆和抛物线方程,得到关于
,分别代入椭圆和抛物线方程,得到关于 的方程组求解即可.
的方程组求解即可.
解题思路:求椭圆的标准方程,往往利用待定系数法进行求解;且要注意隐含条件 .
.
试题解析:(1)据题意得: 又
又 ,
,
解得 ,
,
所以椭圆方程为 .
.
(2)设 点坐标为
点坐标为 ,则
,则 点坐标为
点坐标为 ,分别代入椭圆和抛物线方程得
,分别代入椭圆和抛物线方程得
 消去
消去 并整理得:
并整理得: ,
,
所以 或
或 .
.
当 时,
时, ;
;
当 时,
时, 无解.
无解.
所以直线 的方程为
的方程为 .
.
考点:1.椭圆与抛物线的标准方程;2.待定系数法;3.中点坐标公式.

练习册系列答案
 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
 与两灯塔
与两灯塔 、
、 的距离分别为300米和500米,测得灯塔
的距离分别为300米和500米,测得灯塔 ,灯塔
,灯塔 处,则两灯塔
处,则两灯塔 和
和 的直线与直线
的直线与直线 平行,则
平行,则 的值为( )
的值为( ) B.
B. C.
C. D.
D.
 ,则
,则 ( )
( ) B.
B. C.
C. D.
D.
 ,则
,则 ( )
( ) B、
B、 C、
C、 D、
D、
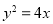 与双曲线
与双曲线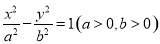 有相同的焦点
有相同的焦点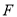 ,点
,点 是两曲线的一个交点,且
是两曲线的一个交点,且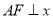 轴,则双曲线的离心率为 .
轴,则双曲线的离心率为 .  ,则
,则 ”及该命题的逆命题、否命题、逆否命题中,真命题的个数为 .
”及该命题的逆命题、否命题、逆否命题中,真命题的个数为 . 相切,则
相切,则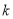 的取值范围是( )
的取值范围是( )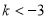 或
或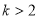
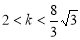
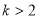 或
或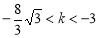
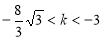 或
或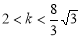
 >0,椭圆
>0,椭圆 的方程为
的方程为 ,双曲线
,双曲线 的方程为
的方程为 ,
, ,则
,则 的渐近线方程为( )
的渐近线方程为( ) B.
B. C.
C. D.
D.