题目内容
如图所示，
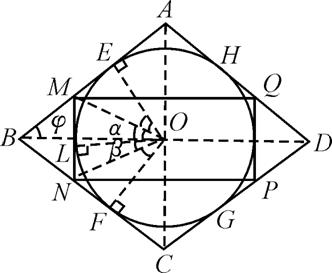
菱形ABCD的内切圆O与各边分别切于E、F、G、H,在
与
上分别作⊙O的切线交AB于M，交BC于N，交CD于P，交DA于Q，求证：MQ∥NP.
证明：
分别连结AC、BD，其交点为内切圆圆心O，设MN与⊙O切于L，分别连结OE、OM、OL、ON、OF，并设∠MOL=α，∠LON=β，∠ABO=φ,则易知∠EOM=α，∠FON=β，∠EOF=2（α+β）,所以∠BOE=∠BOF=α+β，所以∠BON=α,∠CNO=∠AOM.
又∠OCN=∠MAO，于是△OCN∽△MAO，且AM·CN=CO·AO.
同理,AQ·CP=CO·AO，由此可知AM·CN=AQ·CP.
又∠MAQ=∠PCN，有△AMQ∽△CPN，于是，∠AMQ=∠CPN，从而MQ∥NP.
练习册系列答案
相关题目
如图所示，PA⊥平面ABCD，底面ABCD为菱形，∠ABC=60°，PA=AB=2，N为PC的中点．
在如图所示的多面体中，已知正三棱柱ABC-A1B1C1的所有棱长均为2，四边形ABCD是菱形．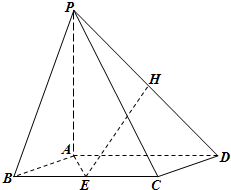
如图所示，在四棱锥P-ABCD中，底面ABCD为菱形，且AB=2，PA⊥平面ABCD，∠ABC=60°，E是BC的中点．
（2011•盐城二模）在如图所示的多面体中，已知正三棱柱ABC-A1B1C1的所有棱长均为2，四边形ABCD是菱形．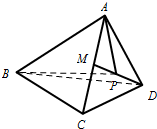
菱形ABCD的边长为
