题目内容
直线ρcosθ-ρsinθ=0的倾斜角是
．
| π |
| 4 |
| π |
| 4 |
分析：先将原极坐标方程ρcosθ-ρsinθ=0，利用直角坐标与极坐标间的关系化成直角坐标方程，再设此直线的倾斜角为θ，则tanθ=1，且 0≤θ＜π，从而得到 θ的值．
解答：解：将原极坐标方程ρcosθ-ρsinθ=0，化成直角坐标方程为：x-y=0，
直线 x-y=0的斜率为 1，设此直线的倾斜角为θ，则tanθ=1，且 0≤θ＜π，
∴θ=
，
故答案为：
．
直线 x-y=0的斜率为 1，设此直线的倾斜角为θ，则tanθ=1，且 0≤θ＜π，
∴θ=
| π |
| 4 |
故答案为：
| π |
| 4 |
点评：本题考查点的极坐标和直角坐标的互化，利用直角坐标与极坐标间的关系，即利用ρcosθ=x，ρsinθ=y，ρ2=x2+y2，进行代换即得．
练习册系列答案
相关题目
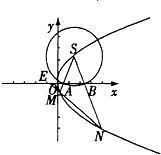已知点F是抛物线C：y2=x的焦点，S是抛物线C在第一象限内的点，且|SF|=
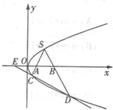如图，S（1，1）是抛物线为y2=2px（p＞0）上的一点，弦SC，SD分别交x小轴于A，B两点，且SA=SB．
的焦点，S是抛物线C在第一象限内的点，且|SF|=
.
轴分别交于两点A、B，延长SA、SB分别交抛物线C于M、N两点；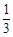
|NE|，求cos∠MSN的值.
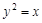的焦点，S是抛物线C在第一象限内的点，且|SF|=
。
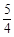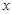轴分别交于两点A、B，延长SA、SB分别交抛物线C于M、N两点；
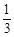|NE|，求cos∠MSN的值。