题目内容
已知幂函数y=f(x)=x-2m2-m+3,其中m∈{x|-2<x<2,x∈Z},满足:
(1)是区间(0,+∞)上的增函数;
(2)对任意的x∈R,都有f(-x)+f(x)=0.
求同时满足(1),(2)的幂函数f(x)的解析式,并求x∈[0,3]时f(x)的值域.
[解析] 由{x|-2<x<2,x∈Z}={-1,0,1}.
(1)由-2m2-m+3>0,
∴2m2+m-3<0,∴- <m<1,∴m=-1或0.
<m<1,∴m=-1或0.
由(2)知f(x)是奇函数.
当m=-1时,f(x)=x2为偶函数,舍去.
当m=0时,f(x)=x3为奇函数.
∴f(x)=x3.
当x∈[0,3]时,f(x)在[0,3]上为增函数,
∴f(x)的值域为[0,27].

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知函数f(x),g(x)分别由下表给出
| x | 1 | 2 | 3 |
| f(x) | 2 | 3 | 1 |
| x | 1 | 2 | 3 |
| g(x) | 3 | 2 | 1 |
则f[g(1)]的值为________;
当g[f(x)]=2时,x=________.
若函数f(x)=x3-x-1在区间[1,1.5]内的一个零点附近函数值用二分法逐次计算列表如下
| x | 1 | 1.5 | 1.25 | 1.375 | 1.3125 |
| f(x) | -1 | 0.875 | -0.2969 | 0.2246 | -0.05151 |
那么方程x3-x-1=0的一个近似根(精确度为0,1)为( )
A.1.2 B.1.3125
C.1.4375 D.1.25
 =
= (a>0),则log
(a>0),则log a=________.
a=________.
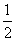
 +θ)=
+θ)=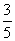 ,则cos(π-2θ)=( )
,则cos(π-2θ)=( ) B.-
B.- D.
D.