题目内容
已知△ABC的内切圆半径为2,且tanA=
解:设AB=c, BC=a, AC=b,D为切点,可知:2AD+2a=a+b+c得:AD=![]() (b+c-a),由tanA=
(b+c-a),由tanA=![]() ,可得:tan∠DAO=2,
,可得:tan∠DAO=2,
所以:DO=b+c-a=2,sinA=![]() .
.
S△ABC=![]() bcsinA=
bcsinA=![]() (a+b+c)?2
(a+b+c)?2
即:![]() bc=2(b+c)-2,所有bc=5(b+c)-5≥10
bc=2(b+c)-2,所有bc=5(b+c)-5≥10![]() -5
-5
设![]() =t,则知:t2-10t+5≥0,所以t≥5+2
=t,则知:t2-10t+5≥0,所以t≥5+2![]() 或t≤5-2
或t≤5-2![]() (舍)
(舍)
故bc≥45+20![]() ,所以S△ABC=
,所以S△ABC=![]() bc≥18+8
bc≥18+8![]() ,b=c=5+2
,b=c=5+2![]() 时取等号。
时取等号。
故△ABC面积的最小值为18+8![]() .
.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
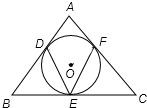 18、已知△ABC的内切圆⊙O如图,若∠DEF=54°,则∠BAC等于
18、已知△ABC的内切圆⊙O如图,若∠DEF=54°,则∠BAC等于
 已知△ABC的内切圆⊙O如图,若∠DEF=54°,则∠BAC等于 ________.
已知△ABC的内切圆⊙O如图,若∠DEF=54°,则∠BAC等于 ________.