题目内容
数列{an}的前n项和为Sn,且
(1)求a1,a2及a3;(2)证明:数列{an}是等比数列,并求an.
解:(1)当n=1时, ,得
,得 ;
;
当n=2时, ,得
,得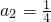 ,同理可得
,同理可得 .
.
(2)当n≥2时, ,
,
∴ ,
,
所以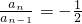 .
.
∵ ,∴
,∴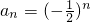 .
.
故数列{an}是等比数列,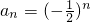 .
.
分析:(1)在 中,分别令n=1,2,3,能够求出a1,a2及a3的值.
中,分别令n=1,2,3,能够求出a1,a2及a3的值.
(2)当n≥2时, ,所以
,所以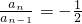 .由此能求出an.
.由此能求出an.
点评:本题考查数列的性质和应用,解题时要认真审题,仔细求解.
 ,得
,得 ;
;当n=2时,
 ,得
,得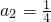 ,同理可得
,同理可得 .
.(2)当n≥2时,
 ,
,∴
 ,
,所以
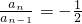 .
.∵
 ,∴
,∴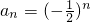 .
.故数列{an}是等比数列,
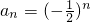 .
.分析:(1)在
 中,分别令n=1,2,3,能够求出a1,a2及a3的值.
中,分别令n=1,2,3,能够求出a1,a2及a3的值.(2)当n≥2时,
 ,所以
,所以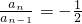 .由此能求出an.
.由此能求出an.点评:本题考查数列的性质和应用,解题时要认真审题,仔细求解.

练习册系列答案
相关题目