Question

已知函数f(x)=

2x-a ，  x≥0 f(x+1)， x＜0

，若方程f（x）+x=0有且仅有两个解，则实数a的取值范围是

 

．

Answer 1

分析：构造函数g（x）=

2x-2，x≥0 g(x+1)，x＜0

，先研究g（x）与y=-x的交点问题，然后利用函数图象之间的平移关系确定a的取值范围．

解答：解：我们先研究g（x）=

2x-2，x≥0 g(x+1)，x＜0

，
①当x≥0时，f（x）=2^x-2，
②当-1≤x＜0时，0≤x+1＜1，g（x）=g（x+1）=2^（x+1）-2．
当-2≤x＜-1时，0≤x+2＜1，g（x）=g（x+2）=2^（x+2）-2．
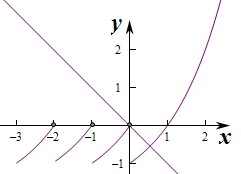
故x＜0时，f（x）是周期函数，如图，
此时函数g（x）与y=-x的图象恰有一个交点
因为函数f(x)=

2x-a ，  x≥0 f(x+1)， x＜0

，的图象是由g（x）=

2x-2，x≥0 g(x+1)，x＜0

向上平移2-a个单位． 
若方程f（x）+x=0有且只有两个不相等的实数根，
则2-a＞0，即a＜2                               
故答案为：a＜2．

点评：本题考查的知识点是函数的图象与图象变化及图象平移，其中根据函数的解析式，分析函数的性质，并画出函数的图象是解答本题的关键．