题目内容
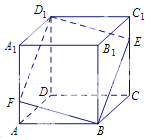
【题目】在三棱柱ABC﹣A1B1C1中,CA=CB,侧面ABB1A1是边长为2的正方形,点E,F分别在线段AA1、A1B1上,且AE= ![]() ,A1F=
,A1F= ![]() ,CE⊥EF.
,CE⊥EF.
(Ⅰ)证明:平面ABB1A1⊥平面ABC;
(Ⅱ)若CA⊥CB,求直线AC1与平面CEF所成角的正弦值.
【答案】证明:(I)取AB的中点D,连结CD,DF,DE. ∵AC=BC,D是AB的中点,∴CD⊥AB.
∵侧面ABB1A1是边长为2的正方形,AE= ![]() ,A1F=
,A1F= ![]() .
.
∴A1E= ![]() ,EF=
,EF= 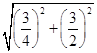 =
= ![]() ,DE=
,DE= 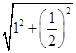 =
= ![]() ,
,
DF= 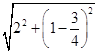 =
= ![]() ,
,
∴EF2+DE2=DF2 , ∴DE⊥EF,
又CE⊥EF,CE∩DE=E,CE平面CDE,DE平面CDE,
∴EF⊥平面CDE,又CD平面CDE,
∴CD⊥EF,
又CD⊥AB,AB平面ABB1A1 , EF平面ABB1A1 , AB,EF为相交直线,
∴CD⊥平面ABB1A1 , 又CDABC,
∴平面ABB1A1⊥平面ABC.
(II)∵平面ABB1A1⊥平面ABC,
∴三棱柱ABC﹣A1B1C1是直三棱柱,∴CC1⊥平面ABC.
∵CA⊥CB,AB=2,∴AC=BC= ![]() .
.
以C为原点,以CA,CB,CC1为坐标轴建立空间直角坐标系,如图所示: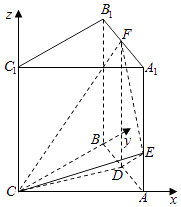
则A( ![]() ,0,0),C(0,0,0),C1(0,0,2),E(
,0,0),C(0,0,0),C1(0,0,2),E( ![]() ,0,
,0, ![]() ),F(
),F( ![]() ,
, ![]() ,2).
,2).
∴ ![]() =(﹣
=(﹣ ![]() ,0,2),
,0,2), ![]() =(
=( ![]() ,0,
,0, ![]() ),
), ![]() =(
=( ![]() ,
, ![]() ,2).
,2).
设平面CEF的法向量为 ![]() =(x,y,z),则
=(x,y,z),则 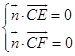 ,
,
∴ 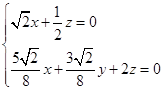 ,令z=4,得
,令z=4,得 ![]() =(﹣
=(﹣ ![]() ,﹣9
,﹣9 ![]() ,4).
,4).
∴ ![]() =10,|
=10,| ![]() |=6
|=6 ![]() ,|
,| ![]() |=
|= ![]() .
.
∴cos< ![]() >=
>= 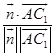 =
= ![]() .
.
∴直线AC1与平面CEF所成角的正弦值为 ![]() .
.
【解析】(I)取AB的中点D,连结CD,DF,DE.计算DE,EF,DF,利用勾股定理的逆定理得出DE⊥EF,由三线合一得CD⊥AB,故而CD⊥平面ABB1A1 , 从而平面ABB1A1⊥平面ABC;(II)以C为原点建立空间直角坐标系,求出 ![]() 和平面CEF的法向量
和平面CEF的法向量 ![]() ,则直线AC1与平面CEF所成角的正弦值等于|cos<
,则直线AC1与平面CEF所成角的正弦值等于|cos< ![]() >|.
>|.

 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案