题目内容
已知函数f(x)=2sinωxcosωx-2cos2ωx(x∈R,ω>0),相邻两条对称轴之间的距离等于 .
.
(Ⅰ)求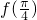 的值;
的值;
(Ⅱ)当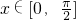 时,求函数f(x)的最大值和最小值及相应的x值.
时,求函数f(x)的最大值和最小值及相应的x值.
解:(Ⅰ) .
.
因为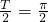 ,所以T=π,ω=1.(3分)
,所以T=π,ω=1.(3分)
所以 .
.
所以 (7分)
(7分)
(Ⅱ)
当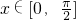 时,
时,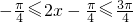 ,(9分)
,(9分)
所以当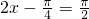 ,即
,即 时,
时, ,(11分)
,(11分)
当 ,即x=0时,f(x)min=-2.(12分)
,即x=0时,f(x)min=-2.(12分)
分析:(I)利用二倍角公式及辅助角公式对函数化简,根据周期公式求ω的值,从而可求f(x),进而可求f( )
)
(Ⅱ)由(I)中函数的解析式,结合正弦函数的性质研究函数的最值及取得最值的条件
点评:本题主要考查了二倍角公式、辅助角公式把不同名的三角函数含为一个角的三角函数,进而研究三角函数的性质:周期性及周期公式,函数的最值的求解.
 .
.因为
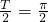 ,所以T=π,ω=1.(3分)
,所以T=π,ω=1.(3分)所以
 .
.所以
 (7分)
(7分)(Ⅱ)

当
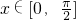 时,
时,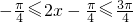 ,(9分)
,(9分)所以当
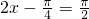 ,即
,即 时,
时, ,(11分)
,(11分)当
 ,即x=0时,f(x)min=-2.(12分)
,即x=0时,f(x)min=-2.(12分)分析:(I)利用二倍角公式及辅助角公式对函数化简,根据周期公式求ω的值,从而可求f(x),进而可求f(
 )
)(Ⅱ)由(I)中函数的解析式,结合正弦函数的性质研究函数的最值及取得最值的条件
点评:本题主要考查了二倍角公式、辅助角公式把不同名的三角函数含为一个角的三角函数,进而研究三角函数的性质:周期性及周期公式,函数的最值的求解.

练习册系列答案
相关题目