题目内容
过原点O的直线l与椭圆C:
+
=1(a>b>0)交于M,N两点,P是椭圆C上异于M,N的任一点.若直线PM,PN的斜率之积为-
,则椭圆C的离心率为
.
| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| 4 |
| ||
| 2 |
| ||
| 2 |
分析:设点的坐标,表示出直线PM,PN的斜率,利用直线PM,PN的斜率之积为-
,结合点差法,化简,即可求得离心率.
| 1 |
| 4 |
解答:解:设P(x,y),M(m,n),N(-m,-n),则直线PM,PN的斜率分别为
,
∵直线PM,PN的斜率之积为-
,∴
•
=-
,∴
•=-
∵M,P是椭圆C上的点
∴
+
=1,
+
=1
两式相减可得
=-
∴
•=-
∴
=
∴a=2b,∴c=
=
b
∴e=
=
故答案为:
| y-n |
| x-m |
| y+n |
| x+m |
∵直线PM,PN的斜率之积为-
| 1 |
| 4 |
| y-n |
| x-m |
| y+n |
| x+m |
| 1 |
| 4 |
| y2-n2 |
| x2-m2 |
| 1 |
| 4 |
∵M,P是椭圆C上的点
∴
| x2 |
| a2 |
| y2 |
| b2 |
| m2 |
| a2 |
| n2 |
| b2 |
两式相减可得
| x2-m2 |
| a2 |
| y2-n2 |
| b2 |
∴
| y2-n2 |
| x2-m2 |
| b2 |
| a2 |
∴
| b2 |
| a2 |
| 1 |
| 4 |
∴a=2b,∴c=
| a2-b2 |
| 3 |
∴e=
| c |
| a |
| ||
| 2 |
故答案为:
| ||
| 2 |
点评:本题考查椭圆的几何性质,考查点差法的运用,考查学生的计算能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
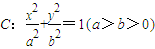 过点
过点 ,离心率
,离心率 ,若点M(x,y)在椭圆C上,则点
,若点M(x,y)在椭圆C上,则点 称为点M的一个“椭点”,直线l交椭圆C于A、B两点,若点A、B的“椭点”分别是P、Q,且以PQ为直径的圆经过坐标原点O.
称为点M的一个“椭点”,直线l交椭圆C于A、B两点,若点A、B的“椭点”分别是P、Q,且以PQ为直径的圆经过坐标原点O. 过点
过点 ,离心率
,离心率 ,若点M(x,y)在椭圆C上,则点
,若点M(x,y)在椭圆C上,则点 称为点M的一个“椭点”,直线l交椭圆C于A、B两点,若点A、B的“椭点”分别是P、Q,且以PQ为直径的圆经过坐标原点O.
称为点M的一个“椭点”,直线l交椭圆C于A、B两点,若点A、B的“椭点”分别是P、Q,且以PQ为直径的圆经过坐标原点O. 和椭圆弧
和椭圆弧
