题目内容

在等差数列{an}中，已知a4=70,a21=-100.

（1）求首项a1与公差d，并写出通项公式;

（2）{an}中有多少项属于区间［-18,18］?

解：（1）由题意，得an=a1+(n-1)d.

∴

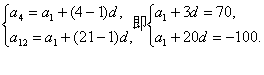
解得a1=100，d=-10.

∴通项公式an=100-10(n-1)=-10n+110.

（2）由题意得-18≤-10n+110≤18，

解得9.2≤n≤12.8.

∵n∈N*，∴n=10,11,12.

∴属于区间［-18，18］的共有3项，它们是a10,a11,a12.


练习册系列答案
相关题目
在等差数列{an}中，a1=-2010，其前n项的和为Sn．若
S2010
2010
-
S2008
2008
=2，则S2010=（　　）
在等差数列{an}中，a1+3a8+a15=60，则2a9-a10的值为
12
12
．
已知在等差数列{an}中，d＞0，a2008、a2009是方程x2-3x-5=0的两个根，那么使得前n项和Sn为负值的最大的n的值是（　　）
在等差数列{an}中，已知a1=2，a2+a3=13，则a4+a5+a6等于=
42
42
．
在等差数列{an}中，若S4=1，S8=4，则a17+a18+a19+a20的值=
9
9
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网