题目内容

设函数y=(tanx+sinx)·(cotx+cosx),且x≠(k∈Z),则关于y的取值范围的判定正确的是(    )

A.y的值恒大于零

B.y的值恒小于零

C.有时大于零,有时等于零,但不小于零

D.有时小于零,有时等于零,但不大于零

解析:y=(tanx+sinx)·(cotx+cosx)=(+sinx)·(+cosx)

=

=(1+cosx)(1+sinx),

又∵x≠(k∈Z),

∴-1＜cosx＜1,-1＜sinx＜1.

∴(1+cosx)(1+sinx)＞0,即y＞0.

答案:A

练习册系列答案
相关题目
给出下列五个命题：
①函数y=tanx的图象关于点（kπ+
π
2
，0）（k∈Z）对称；
②函数f（x）=sin|x|是最小正周期为π的周期函数；
③设θ为第二象限的角，则tan
θ
2
＞cos
θ
2
，且sin
θ
2
＞cos
θ
2
；
④函数y=cos2x+sinx的最小值为-1．
其中正确的命题是
①④
①④
．
设函数y=lg（tanx-1），则该函数的定义域为
{x|kπ+
π
4
＜x＜kπ+
π
2
，k∈Z}
{x|kπ+
π
4
＜x＜kπ+
π
2
，k∈Z}
．
设函数y=(tanx+sinx)·(cotx+cosx),且x≠(k∈Z),则关于y的取值范围的判定正确的是(    )

A.y的值恒大于零

B.y的值恒小于零

C.有时大于零,有时等于零,但不小于零

D.有时小于零,有时等于零,但不大于零

给出下列五种说法：

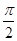①函数y=-sin(kπ+x)(k∈Z)是奇函数；②函数y=tanx的图象关于点(kπ+,0)(k∈Z)对称；③函数f(x)=sin|x|是最小正周期为π的周期函数；④设θ为第二象限角，则tan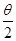＞cos，且sin＞cos；⑤函数y=cos2x+sinx的最小值为-1.

其中正确的是.____________________

 

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网