题目内容
已知函数f(x)= ,若f(x)-kx有三个零点,则k的取值范围为 .
,若f(x)-kx有三个零点,则k的取值范围为 .
【答案】分析:由题意画出图象,利用导数对x分x=0、x<0、x>0三种情况各有一个零点时的k的取值范围求出来,再求交集即可.
解答:解:由题意画出图象: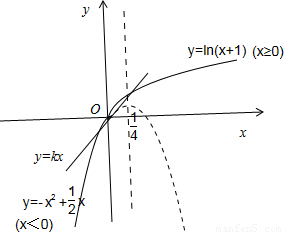
(1)当x=0时,f(0)=ln1=0,k×0=0,0是函数f(x)-kx的一个零点;
(2)由函数的图象和单调性可以看出,当x>0和x<0时,分别有一个零点.
①.当x<0时,由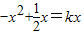 ,化为
,化为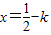 <0,解得
<0,解得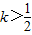 ;
;
②当x>0时,只考虑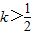 即可,
即可,
令g(x)=ln(x+1)-kx,则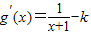 ,
,
A.当k≥1时,则g′(x)<0,即g(x)在(0,+∞)上单调递减,∴g(x)<g(0)=0,g(x)无零点,应舍去;
B.当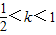 时,
时,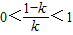 ,
,
g′(x)=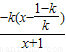 ,令g′(x)=0,解得
,令g′(x)=0,解得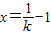 ,列表如下:
,列表如下: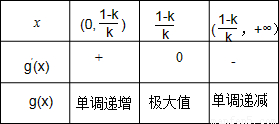
由表格可知:当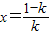 时,g(x)取得极大值,也是最大值,当且仅当
时,g(x)取得极大值,也是最大值,当且仅当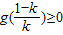 时,g(x)才有零点,
时,g(x)才有零点,
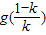 =
=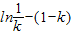 =k-lnk-1.
=k-lnk-1.
下面证明h(k)=k-lnk-1>0,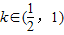 .
.
∵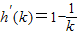 =
=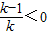 ,∴h(k)在
,∴h(k)在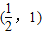 上单调递减,∴
上单调递减,∴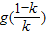 =h(k)>h(1)=1-ln1-1=0,
=h(k)>h(1)=1-ln1-1=0,
因此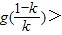 0在
0在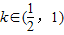 时成立.
时成立.
综上可知:当且仅当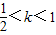 时,函数f(x)-kx有三个零点.
时,函数f(x)-kx有三个零点.
点评:熟练掌握利用导数研究函数的单调性、极值和最值的方法及数形结合、分类讨论的思想方法是解题的关键.
解答:解:由题意画出图象:

(1)当x=0时,f(0)=ln1=0,k×0=0,0是函数f(x)-kx的一个零点;
(2)由函数的图象和单调性可以看出,当x>0和x<0时,分别有一个零点.
①.当x<0时,由
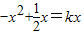 ,化为
,化为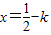 <0,解得
<0,解得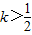 ;
;②当x>0时,只考虑
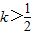 即可,
即可,令g(x)=ln(x+1)-kx,则
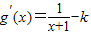 ,
,A.当k≥1时,则g′(x)<0,即g(x)在(0,+∞)上单调递减,∴g(x)<g(0)=0,g(x)无零点,应舍去;
B.当
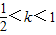 时,
时,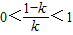 ,
,g′(x)=
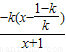 ,令g′(x)=0,解得
,令g′(x)=0,解得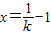 ,列表如下:
,列表如下:
由表格可知:当
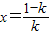 时,g(x)取得极大值,也是最大值,当且仅当
时,g(x)取得极大值,也是最大值,当且仅当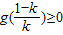 时,g(x)才有零点,
时,g(x)才有零点,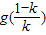 =
=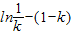 =k-lnk-1.
=k-lnk-1.下面证明h(k)=k-lnk-1>0,
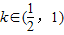 .
.∵
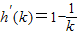 =
=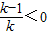 ,∴h(k)在
,∴h(k)在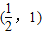 上单调递减,∴
上单调递减,∴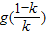 =h(k)>h(1)=1-ln1-1=0,
=h(k)>h(1)=1-ln1-1=0,因此
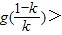 0在
0在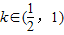 时成立.
时成立.综上可知:当且仅当
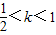 时,函数f(x)-kx有三个零点.
时,函数f(x)-kx有三个零点.点评:熟练掌握利用导数研究函数的单调性、极值和最值的方法及数形结合、分类讨论的思想方法是解题的关键.

练习册系列答案
 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
已知函数f(x)=x2-bx的图象在点A(1,f(1))处的切线l与直线3x-y+2=0平行,若数列{
}的前n项和为Sn,则S2010的值为( )
| 1 |
| f(n) |
A、
| ||
B、
| ||
C、
| ||
D、
|