题目内容
已知关于x的三次函数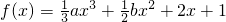 在区间(1,2)上只有极大值,则b-a的取值范围是
在区间(1,2)上只有极大值,则b-a的取值范围是
- A.(-1,+∞)
- B.(-2,+∞)
- C.(-3,+∞)
- D.(-4,+∞)
D
分析:极大值是函数先增再减,相应导数是先增后负得不等式组再利用线性规划解
解答:f′(x)=ax2+bx+2
∵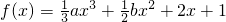 在区间(1,2)上只有极大值
在区间(1,2)上只有极大值
∴ 即
即
∴-4<b-a
故选项为D
点评:函数在某点处取极值的条件,利用线性规划求范围
分析:极大值是函数先增再减,相应导数是先增后负得不等式组再利用线性规划解
解答:f′(x)=ax2+bx+2
∵
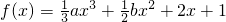 在区间(1,2)上只有极大值
在区间(1,2)上只有极大值∴
 即
即
∴-4<b-a
故选项为D
点评:函数在某点处取极值的条件,利用线性规划求范围

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
已知关于x的三次函数f(x)=
ax3+
bx2+2x+1在区间(1,2)上只有极大值,则b-a的取值范围是( )
| 1 |
| 3 |
| 1 |
| 2 |
| A、(-1,+∞) |
| B、(-2,+∞) |
| C、(-3,+∞) |
| D、(-4,+∞) |
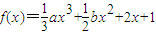 在区间(1,2)上只有极大值,则b-a的取值范围是( )
在区间(1,2)上只有极大值,则b-a的取值范围是( ) 在区间(1,2)上有且只有一个极大值,则b-a的取值范围是
在区间(1,2)上有且只有一个极大值,则b-a的取值范围是