题目内容
过双曲线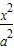 -
-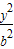 =1(a>0,b>0)的右顶点A作斜率为-1的直线,该直线与双曲线的两条渐近线的交点分别为B、C.若
=1(a>0,b>0)的右顶点A作斜率为-1的直线,该直线与双曲线的两条渐近线的交点分别为B、C.若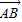 =
=
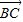 ,则双曲线的离心率是( )
,则双曲线的离心率是( )A.
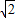
B.
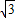
C.
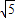
D.
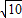
【答案】分析:分别表示出直线l和两个渐进线的交点,进而表示出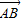 和
和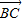 ,进而根据
,进而根据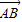 =
=
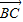 求得a和b的关系,进而根据c2-a2=b2,求得a和c的关系,则离心率可得.
求得a和b的关系,进而根据c2-a2=b2,求得a和c的关系,则离心率可得.
解答:解:直线l:y=-x+a与渐近线l1:bx-ay=0交于B(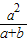 ,
,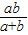 ),
),
l与渐近线l2:bx+ay=0交于C(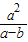 ,
,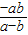 ),A(a,0),
),A(a,0),
∴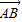 =(-
=(-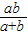 ,
,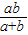 ),
),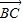 =(
=(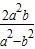 ,-
,-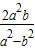 ),∵
),∵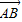 =
=
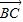 ,
,
∴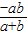 =
=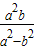 ,b=2a,
,b=2a,
∴c2-a2=4a2,
∴e2=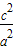 =5,∴e=
=5,∴e=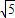 ,
,
故选C.
点评:本题主要考查了直线与圆锥曲线的综合问题.要求学生有较高地转化数学思想的运用能力,能将已知条件转化到基本知识的运用.
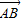 和
和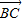 ,进而根据
,进而根据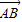 =
=
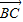 求得a和b的关系,进而根据c2-a2=b2,求得a和c的关系,则离心率可得.
求得a和b的关系,进而根据c2-a2=b2,求得a和c的关系,则离心率可得.解答:解:直线l:y=-x+a与渐近线l1:bx-ay=0交于B(
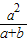 ,
,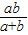 ),
),l与渐近线l2:bx+ay=0交于C(
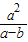 ,
,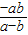 ),A(a,0),
),A(a,0),∴
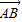 =(-
=(-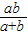 ,
,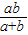 ),
),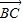 =(
=(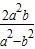 ,-
,-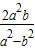 ),∵
),∵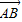 =
=
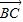 ,
,∴
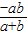 =
=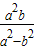 ,b=2a,
,b=2a,∴c2-a2=4a2,
∴e2=
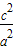 =5,∴e=
=5,∴e=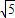 ,
,故选C.
点评:本题主要考查了直线与圆锥曲线的综合问题.要求学生有较高地转化数学思想的运用能力,能将已知条件转化到基本知识的运用.

练习册系列答案
相关题目
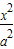 -
-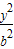 =1(a>0,b>0)的一个焦点F引它到渐进线的垂线,垂足为M,延长FM交y轴于E,若
=1(a>0,b>0)的一个焦点F引它到渐进线的垂线,垂足为M,延长FM交y轴于E,若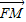 =2
=2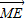 ,则该双曲线离心率为( )
,则该双曲线离心率为( )
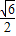
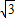
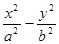 =1(a>0,b>0)的左焦点F(-c,0)(c>0),作圆
=1(a>0,b>0)的左焦点F(-c,0)(c>0),作圆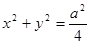 的切线,切点为E,延长FE交双曲线右支于点P,若
的切线,切点为E,延长FE交双曲线右支于点P,若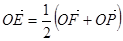 ,则双曲线的离心率为( )
,则双曲线的离心率为( )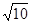 B.
B.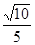 C.
C.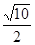 D.
D.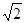
 -
- =1(a>0,b>0)的一个焦点,并与双曲线实轴垂直,已知抛物线与双曲线的一个交点为(
=1(a>0,b>0)的一个焦点,并与双曲线实轴垂直,已知抛物线与双曲线的一个交点为( ,
, ),求抛物线与双曲线方程.
),求抛物线与双曲线方程. -
-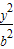 =1(a>0,b>0)的右顶点A作斜率为-1的直线,该直线与双曲线的两条渐近线的交点分别为B、C.若
=1(a>0,b>0)的右顶点A作斜率为-1的直线,该直线与双曲线的两条渐近线的交点分别为B、C.若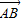 =
=
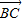 ,则双曲线的离心率是( )
,则双曲线的离心率是( )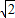
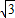
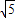
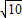
 -
- =1(a>0,b>0)的右焦点且与双曲线的两条渐近线分别交于A,B两点,若原点在以AB为直径的圆外,则双曲线离心率的取值范围是 .
=1(a>0,b>0)的右焦点且与双曲线的两条渐近线分别交于A,B两点,若原点在以AB为直径的圆外,则双曲线离心率的取值范围是 .