题目内容
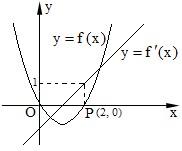13、已知函数Y=f（x）及其导函数Y=F′（x）的图象如图所示，则曲线y=f（x）在点P处的切线方程是x-y-2=0
．分析：根据图象找出P的坐标，即为切点坐标，由导函数的图象可知x=2时，导函数值为1，即切线方程的斜率为1，根据切点坐标和斜率写出切线方程即可．
解答：解：根据图象可知P坐标为（2，0），
且f′（2）=1，即切线的斜率k=1，
则曲线y=f（x）在点P处的切线方程是y=x-2，即x-y-2=0．
故答案为：x-y-2=0
且f′（2）=1，即切线的斜率k=1，
则曲线y=f（x）在点P处的切线方程是y=x-2，即x-y-2=0．
故答案为：x-y-2=0
点评：此题考查了利用导数研究曲线上某点的切线方程，考查了数形结合的思想．借助图象找出切点坐标和切线斜率是解本题的关键．
练习册系列答案
小学生10分钟口算测试100分系列答案
相关题目
已知函数y=f（x）是定义在R上的奇函数，当x＞0 时，f（x）的图象如图所示，则不等式x[f（x）-f（-x）]≤0 的解集为
已知函数y=f（x）的图象如图，则满足