题目内容
已知函数y=Asin(ωx+φ)(A>0,ω>0,-(1)求这个函数的表达式;
(2)求这个函数的单调区间.
解析:根据题意确定A及最小正周期T,然后列出方程求出结论.?
(1)由题意知,A=![]() ,
,![]() =6-2=4,?
=6-2=4,?
∴T=16=![]() . ∴ω=
. ∴ω=![]() .?
.?
又∵函数图象经过Q(6,0),?
∴0=![]() sin(
sin(![]() ×6+φ),-
×6+φ),- ![]() <x<
<x<![]() .?
.?
∴φ=![]() .?
.?
∴函数表达式为y=![]() sin(
sin(![]() x+
x+![]() ).?
).?
(2)令2kπ-![]() ≤
≤![]() x+
x+![]() ≤2kπ+
≤2kπ+![]() ,k∈Z,?
,k∈Z,?
解得16k-6≤x≤16k+2,k∈Z,?
∴函数y=![]() sin(
sin(![]() x+
x+![]() )的单调递增区间为[16k-6,16k+2],k∈Z.?
)的单调递增区间为[16k-6,16k+2],k∈Z.?
同理可得函数y=![]() sin(
sin(![]() x+
x+![]() )的单调递减区间为[16k+2,16k+10],k∈Z.
)的单调递减区间为[16k+2,16k+10],k∈Z.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案
相关题目
已知函数y=Asin(ωx+φ),在同一周期内,当x=
时,取最大值y=2,当x=
时,取得最小值y=-2,那么函数的解析式为( )
| π |
| 12 |
| 7π |
| 12 |
A、y=
| ||||
B、y=2sin(2x+
| ||||
C、y=2sin(
| ||||
D、y=2sin(2x+
|
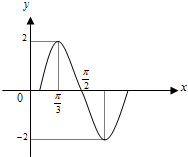 已知函数y=Asin(ωx+∅)(A>0,ω>0,-π≤∅≤π)一个周期的图象(如图),则这个函数的一个解析式为( )
已知函数y=Asin(ωx+∅)(A>0,ω>0,-π≤∅≤π)一个周期的图象(如图),则这个函数的一个解析式为( )A、y=2sin(
| ||||
B、y=2sin(3x+
| ||||
C、y=2sin(3x-
| ||||
D、y=2sin(3x-
|
 已知函数
已知函数 已知函数
已知函数