题目内容
三棱锥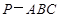
的四个顶点都在体积为
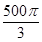的球的表面上，底面ABC所在的小圆面积为16π，则该三棱锥的高的最大值为( )
A．7 B．7.5 C．8 D．9
【答案】
C
【解析】
试题分析：由
求得球的半径为
，由
求得底面ABC所在的小圆的半径
，则球心O到底面ABC所在小圆的圆心H的距离
。当点P在底面ABC的投影与C重合时，该三棱锥的高最大，求得最大值为
。故选C。
考点：棱柱、棱锥、棱台的体积；球内接多面体．
点评：本题考查了由球的体积求半径，由圆的面积求半径，以及勾股定理的应用，是基础题．
练习册系列答案
相关题目
一个正三棱锥的四个顶点都在半径为1的球面上，其中底面的三个顶点在该球的一个大圆上，则该正三棱锥的体积是（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
底面边长为
，各侧面均为直角三角形的正三棱锥的四个顶点都在同一球面上，则此球的表面积为（ ）
| 2 |
| A、4π | ||
B、
| ||
| C、2π | ||
| D、3π |